Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp cho các em đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này ngay nhé!
Cho tam giác ABC có AB = AC = 13 cm, Bc = 10 cm và có BH, CK là hai đường cao. Chứng minh: a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O;R). b) Điểm A nằm ngoài đường tròn (O; R).
Đề bài
Cho tam giác ABC có AB = AC = 13 cm, Bc = 10 cm và có BH, CK là hai đường cao. Chứng minh:
a) Bốn điểm B, C, H, K cùng nằm trên đường tròn (O;R).
b) Điểm A nằm ngoài đường tròn (O; R).
Phương pháp giải - Xem chi tiết
Dựa vào: Đường tròn tâm O bán kính R (R > 0) là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
Chứng minh OA > R thì điểm A nằm ngoài đường tròn (O; R).
Lời giải chi tiết
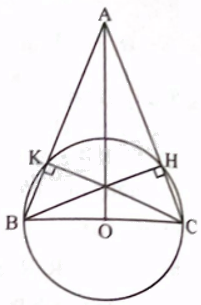
a) Gọi O là trung điểm của BC.
Trong các tam giác vuông BHC và BKC ta có OH = OK = OB = OC = 5 cm, suy ra bốn điểm B, C, H, K cùng nằm trên đường tròn (O; R) với R = 5 cm.
b) Ta có:
\(OA = \sqrt {B{A^2} - O{B^2}} = \sqrt {{{13}^2} - {5^2}} = 12(cm).\)
Vì 12 > 5 nên OA > R, suy ra điểm A nằm ngoài đường tròn (O;R).
Bài 2 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc.
Bài 2 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài 2 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1, chúng ta cần nắm vững các kiến thức sau:
Để xác định hệ số góc của đường thẳng, ta chỉ cần nhìn vào phương trình của đường thẳng. Ví dụ, nếu đường thẳng có phương trình y = 2x + 3, thì hệ số góc là 2.
Để tìm đường thẳng song song với một đường thẳng cho trước, ta chỉ cần giữ nguyên hệ số góc của đường thẳng đó và thay đổi tung độ gốc. Ví dụ, nếu đường thẳng cho trước có phương trình y = 2x + 3, thì một đường thẳng song song có thể có phương trình y = 2x + 5.
Để tìm đường thẳng vuông góc với một đường thẳng cho trước, ta lấy nghịch đảo có dấu âm của hệ số góc của đường thẳng đó. Ví dụ, nếu đường thẳng cho trước có phương trình y = 2x + 3, thì hệ số góc của đường thẳng vuông góc là -1/2. Do đó, phương trình của đường thẳng vuông góc có thể là y = -1/2x + 1.
Để xác định giao điểm của hai đường thẳng, ta giải hệ phương trình gồm phương trình của hai đường thẳng đó. Giao điểm là nghiệm của hệ phương trình.
Giả sử chúng ta có đường thẳng y = 3x - 2. Hãy tìm một đường thẳng song song và một đường thẳng vuông góc với đường thẳng này.
Để củng cố kiến thức về hàm số bậc nhất và các tính chất của đường thẳng, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 9 Chân trời sáng tạo tập 1.
Bài 2 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp các em hiểu sâu hơn về hàm số bậc nhất và các tính chất của đường thẳng. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.