Bài 4 trang 103 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 103, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
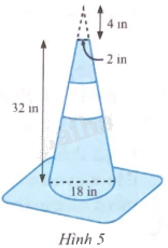
Một cọc tiêu có dạng hình nón bị cắt đi phần ở trên cũng có dạng hình nón như Hình 5. a) Tính diện tích xung quanh của cọc tiêu theo đơn vị in2 (không tính phần đế). b) Tính thể tích của cọc tiêu theo đơn vị in3 (không tính phần đế). (Làm tròn kết quả đến hàng đơn vị của in2, in3).
Đề bài
Một cọc tiêu có dạng hình nón bị cắt đi phần ở trên cũng có dạng hình nón như Hình 5.
a) Tính diện tích xung quanh của cọc tiêu theo đơn vị in2 (không tính phần đế).
b) Tính thể tích của cọc tiêu theo đơn vị in3 (không tính phần đế).
(Làm tròn kết quả đến hàng đơn vị của in2, in3).
Phương pháp giải - Xem chi tiết
Diện tích xung quanh hình nón: \({S_{xq}} = \pi rl\).
Thể tích của hình nón: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
a) Độ dài đường sinh của hình nón bị cắt đi là: \({l_1} = \sqrt {{1^2} + {4^2}} = \sqrt {17} \) (in)
Diện tích xung quanh hình nón bị cắt đi là: \({S_1} = \pi r{l_1} = \pi .1.\sqrt {17} = \pi \sqrt {17} \) (in2).
Độ dài đường sinh của hình nón chưa bị cắt đi là: \({l_2} = \sqrt {{{36}^2} + {9^2}} = 9\sqrt {17} \) (in)
Diện tích xung quanh hình nón chưa bị cắt đi là: \({S_2} = \pi r{l_1} = \pi .9.9\sqrt {17} = 81\pi \sqrt {17} \)(in2).
Diện tích xung quanh của cọc tiêu là: \({S_2} - {S_1} = 81\pi \sqrt {17} - \pi \sqrt {17} \approx 1036\)(in2).
b) Thể tích của hình nón bị cắt đi là: \({V_1} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.1^2}.4 = \frac{4}{3}\pi \) (in3).
Thể tích của hình nón chưa bị cắt đi là: \({V_2} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.9^2}.36 = 972\pi \) (in3).
Thể tích của cọc tiêu là: \({V_2} - {V_1} = 972\pi - \frac{4}{3}\pi \approx 3049\)(in3).
Bài 4 trang 103 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương Hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Bài 4 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Cụ thể, bài toán có thể mô tả một tình huống như quỹ đạo của một vật được ném lên, hoặc sự thay đổi của một đại lượng theo thời gian.
Để giải bài 4 trang 103, ta thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm chiều cao lớn nhất mà một quả bóng có thể đạt được khi được ném lên. Ta có hàm số mô tả chiều cao của quả bóng là h(t) = -5t2 + 20t, với t là thời gian tính bằng giây.
Để tìm chiều cao lớn nhất, ta tìm đỉnh của parabol:
x = -b/2a = -20/(2*(-5)) = 2
h(2) = -5*(2)2 + 20*2 = 20
Vậy chiều cao lớn nhất mà quả bóng có thể đạt được là 20 mét.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc hai, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Bài 4 trang 103 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin hơn khi giải bài tập này.
| Công thức | Mô tả |
|---|---|
| x = -b/2a | Hoành độ đỉnh của parabol |
| y = ax2 + bx + c | Dạng tổng quát của hàm số bậc hai |