Bài 14 trang 48 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 14 trang 48, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho Hình 2. Biết tam giác đều ABC có độ dài đường cao AH bằng (11sqrt 3 ). Tính độ dài cạnh của tam giác đó.
Đề bài
Cho Hình 2. Biết tam giác đều ABC có độ dài đường cao AH bằng \(11\sqrt 3 \). Tính độ dài cạnh của tam giác đó.
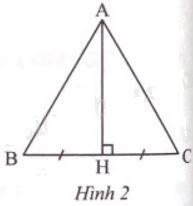
Phương pháp giải - Xem chi tiết
Gọi x là độ dài cạnh của tam giác ABC (x > 0).
Dựa vào dữ kiện đề bài để tìm cạnh tam giác ABC theo x.
Lời giải chi tiết
Gọi x là độ dài cạnh của tam giác ABC (x > 0).
Ta có AB = x, BH = \(\frac{x}{2}\).
Tam giác vuông ABH vuông tại H nên AB2 – BH2 = AH2 hay \({x^2} - {\left( {\frac{x}{2}} \right)^2} = {\left( {11\sqrt 3 } \right)^2}.\)
Suy ra x2 = 112 . 22 hay x = 11. 2 = 22.
Trước khi đi vào giải chi tiết bài 14 trang 48, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất. Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. Đồ thị của hàm số bậc nhất là một đường thẳng. Để vẽ đồ thị hàm số, ta cần xác định hai điểm thuộc đồ thị. Việc hiểu rõ các tính chất của hàm số bậc nhất là nền tảng để giải quyết các bài toán liên quan.
Bài 14 trang 48 yêu cầu chúng ta giải các bài toán liên quan đến việc xác định hệ số a và b của hàm số bậc nhất dựa trên các thông tin cho trước. Thông thường, các bài toán này sẽ cung cấp các điểm mà đồ thị hàm số đi qua hoặc các điều kiện liên quan đến hệ số a và b.
Để xác định hàm số y = ax + b khi biết hai điểm thuộc đồ thị, ta thực hiện các bước sau:
Ví dụ, nếu đồ thị hàm số đi qua hai điểm A(1; 2) và B(2; 5), ta có:
Giải hệ phương trình:
| a | b | ||
|---|---|---|---|
| a + b | 1 | 1 | 2 |
| 2a + b | 2 | 1 | 5 |
Trừ phương trình thứ nhất cho phương trình thứ hai, ta được: a = 3. Thay a = 3 vào phương trình a + b = 2, ta được b = -1. Vậy hàm số cần tìm là y = 3x - 1.
Nếu biết hệ số a và một điểm thuộc đồ thị, ta thực hiện các bước sau:
Ví dụ, nếu a = 2 và đồ thị hàm số đi qua điểm C(-1; 3), ta có:
3 = 2(-1) + b => 3 = -2 + b => b = 5. Vậy hàm số cần tìm là y = 2x + 5.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 14 trang 48 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và cách xác định hàm số. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em tự tin hơn trong quá trình học tập môn Toán.