Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 93 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để các em hiểu rõ bản chất của bài toán.
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của (widehat {OBO'}) cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh (widehat {BOC}) và (widehat {BO'D}).
Đề bài
Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của \(\widehat {OBO'}\) cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh \(\widehat {BOC}\) và \(\widehat {BO'D}\).
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {OBC} = \widehat {OCB} = \widehat {CBO'} = \widehat {O'DB}\) sau đó so sánh \(\widehat {BOC}\) và \(\widehat {BO'D}\).
Lời giải chi tiết
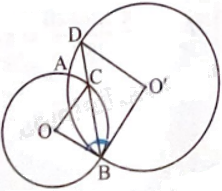
Ta có \(\widehat {OBC} = \widehat {CBO'}\) (vì BC là đường phân giác của \(\widehat {OBO'}\)).
Ta lại có \(\widehat {OBC} = \widehat {OCB}\) (vì tam giác OBC cân tại O),
\(\widehat {CBO'} = \widehat {O'DB}\) (vì tam giác O’BD cân tại O’).
Suy ra \(\widehat {OBC} = \widehat {OCB} = \widehat {CBO'} = \widehat {O'DB}\),
\(\widehat {BOC} = \widehat {BO'D}\).
Bài 4 trang 93 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 4 bao gồm các ý nhỏ khác nhau, mỗi ý tập trung vào một khía cạnh cụ thể của hàm số bậc nhất. Các ý thường yêu cầu:
Để giải bài 4 trang 93 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 hiệu quả, học sinh cần nắm vững các kiến thức sau:
Bài 4a: Cho hàm số y = 2x + 1. Tính giá trị của y khi x = -1.
Giải: Thay x = -1 vào hàm số y = 2x + 1, ta được: y = 2*(-1) + 1 = -2 + 1 = -1. Vậy, khi x = -1 thì y = -1.
Bài 4b: Cho hàm số y = -3x + 5. Tính giá trị của y khi x = 2.
Giải: Thay x = 2 vào hàm số y = -3x + 5, ta được: y = -3*(2) + 5 = -6 + 5 = -1. Vậy, khi x = 2 thì y = -1.
Bài 4c: Xác định hệ số a của hàm số y = ax + 2, biết rằng đồ thị của hàm số đi qua điểm A(1; 3).
Giải: Vì đồ thị của hàm số đi qua điểm A(1; 3) nên tọa độ của điểm A thỏa mãn phương trình y = ax + 2. Thay x = 1 và y = 3 vào phương trình, ta được: 3 = a*(1) + 2. Suy ra a = 3 - 2 = 1. Vậy, a = 1.
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 và các nguồn tài liệu học tập trực tuyến khác.
Bài 4 trang 93 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn trong quá trình học tập và làm bài tập Toán 9.