Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 79 sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin giải quyết các bài toán tương tự.
Cho hình chữ nhật ABCD có AB = 5 cm, AD = 12 cm. Tìm tâm và bán kính của đường tròn ngoại tiếp các tam giác ABC và ADC.
Đề bài
Cho hình chữ nhật ABCD có AB = 5 cm, AD = 12 cm. Tìm tâm và bán kính của đường tròn ngoại tiếp các tam giác ABC và ADC.
Phương pháp giải - Xem chi tiết
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm cạnh huyền và bán kính bằng nửa cạnh huyền.
Lời giải chi tiết
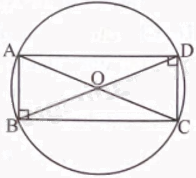
Hai tam giác vuông ABC và ADC có chung cạnh huyền AC nên chúng có cùng có đường tròn ngoại tiếp là (O; R) với tâm O là trung điểm của AC và bán kính
R = \(\frac{{AC}}{2} = \frac{{\sqrt {A{B^2} + B{C^2}} }}{2} = \frac{{\sqrt {{5^2} + {{12}^2}} }}{2} = \frac{{13}}{2} = 6,5\) (cm).
Bài 3 trang 79 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, liên quan đến việc xác định hàm số, tính giá trị của hàm số và ứng dụng hàm số vào các bài toán hình học.
Bài 3 bao gồm các ý nhỏ khác nhau, mỗi ý tập trung vào một khía cạnh cụ thể của hàm số bậc nhất. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản sau:
Để xác định hàm số bậc nhất, học sinh cần kiểm tra xem biểu thức đã cho có dạng y = ax + b (a ≠ 0) hay không. Nếu có, thì a và b là các hệ số của hàm số. Ví dụ, nếu biểu thức là y = 2x + 3, thì a = 2 và b = 3.
Để tính giá trị của hàm số tại một điểm x nào đó, học sinh chỉ cần thay giá trị của x vào biểu thức của hàm số và tính toán kết quả. Ví dụ, nếu hàm số là y = 2x + 3 và x = 1, thì y = 2(1) + 3 = 5.
Trong các bài toán hình học, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa các đại lượng hình học, chẳng hạn như chiều dài, chiều rộng, diện tích, chu vi. Học sinh cần phân tích bài toán để xác định các đại lượng liên quan và xây dựng hàm số phù hợp.
Bài toán: Một người đi xe đạp với vận tốc không đổi là 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó sau t giờ.
Giải: Gọi s là quãng đường đi được của người đó sau t giờ. Vì vận tốc không đổi là 15 km/h, nên quãng đường đi được tỉ lệ thuận với thời gian. Do đó, hàm số biểu thị quãng đường đi được là s = 15t.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể tự giải các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Ngoài ra, các em cũng có thể tham khảo các tài liệu học tập trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Bài 3 trang 79 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu sắc về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng rằng với lời giải chi tiết và hướng dẫn giải cụ thể trong bài viết này, các em sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán 9.