Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 106 sách bài tập toán 9 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
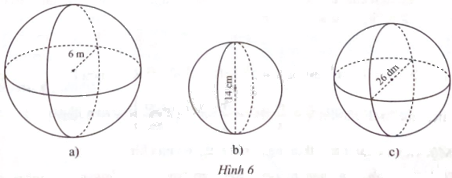
Tính diện tích mặt cầu và thể tích của mỗi hình cầu sau:
Đề bài
Tính diện tích mặt cầu và thể tích của mỗi hình cầu sau:
Phương pháp giải - Xem chi tiết
Diện tích mặt cầu là: \(S = 4\pi {R^2}\).
Thể tích hình cầu là: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết
a) Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4.\pi {.6^2} = 144\pi \) (m2).
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.6^3} = 288\pi \) (m3).
b) Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4.\pi {.7^2} = 196\pi \) (cm2).
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.7^3} = \frac{{1372\pi }}{3}\) (cm3).
c) Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4.\pi {.13^2} = 676\pi \) (dm2).
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.13^3} = \frac{{8788\pi }}{3}\) (dm3).
Bài 1 trang 106 sách bài tập toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 trang 106 sách bài tập toán 9 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 106 sách bài tập toán 9 - Chân trời sáng tạo tập 2 một cách hiệu quả, bạn có thể làm theo các bước sau:
Bài toán: Cho hàm số y = 2x - 1. Tìm tọa độ giao điểm của đường thẳng này với đường thẳng y = -x + 2.
Giải:
Để tìm tọa độ giao điểm của hai đường thẳng, ta giải hệ phương trình sau:
| y = 2x - 1 | y = -x + 2 |
Thay y = 2x - 1 vào phương trình y = -x + 2, ta được:
2x - 1 = -x + 2
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x - 1, ta được:
y = 2(1) - 1 = 1
Vậy tọa độ giao điểm của hai đường thẳng là (1; 1).
Bài 1 trang 106 sách bài tập toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!