Bài 2 trang 72 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số, đồ thị hàm số và các tính chất của hàm số để tìm ra lời giải chính xác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 72 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
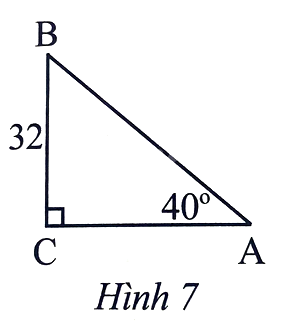
Tính cạnh AC của tam giác vuông trong Hình 7.
Đề bài
Tính cạnh AC của tam giác vuông trong Hình 7.
Phương pháp giải - Xem chi tiết
Dựa vào: Mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với cosin góc kề.
Mỗi cạnh góc vuông bằng cạnh góc vuông nhân với tang góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết
AC = BC. cot A = 32. cot 40o\( \approx 38,14\).
Bài 2 trang 72 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc và tung độ gốc của đường thẳng, viết phương trình đường thẳng khi biết các yếu tố khác nhau, và ứng dụng các kiến thức này vào giải quyết các bài toán thực tế.
Thông thường, bài 2 trang 72 sẽ bao gồm các dạng bài tập sau:
Để giải bài 2 trang 72 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, các em cần nắm vững các kiến thức sau:
Ví dụ, xét bài toán sau:
Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(-1; 0).
Giải:
1. Tính hệ số góc: a = (y2 - y1) / (x2 - x1) = (0 - 2) / (-1 - 1) = 1
2. Sử dụng điểm A(1; 2) để tìm tung độ gốc: 2 = 1 * 1 + b => b = 1
3. Phương trình đường thẳng: y = x + 1
Để giải nhanh các bài tập về hàm số bậc nhất, các em nên:
Khi giải bài tập về hàm số bậc nhất, các em cần chú ý:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 hoặc trên các trang web học toán online.
Bài 2 trang 72 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và các mẹo giải nhanh mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.