Bài 14 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc, đường thẳng song song và các tính chất liên quan.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 14 trang 74, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giải các tam giác vuông trong Hình 7.
Đề bài
Giải các tam giác vuông trong Hình 7.
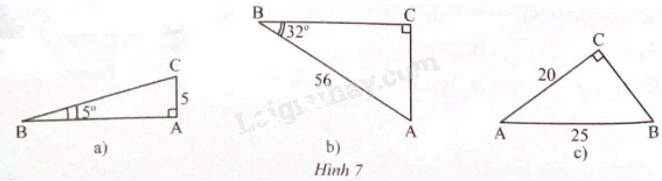
Phương pháp giải - Xem chi tiết
Giải tam giác vuông là tính các cạnh và các góc chưa biết của tam giác đó.
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
a) \(\widehat C = {90^o} - {15^o} = {75^o};\)
\(AB = 5.\cot {15^o} \approx 18,66;\)
\(BC = \frac{5}{{\sin {{15}^o}}} \approx 19,32;\)
b) \(\widehat A = {90^o} - {32^o} = {58^o};\)
\(AC = 56.\sin {32^o} \approx 29,68;\)
\(BC = 56.c{\rm{os3}}{{\rm{2}}^o} \approx 47,49;\)
c) \(BC = \sqrt {A{B^2} - A{C^2}} = \sqrt {{{25}^2} - {{20}^2}} = 15;\)
\(\sin A = \frac{{15}}{{25}} = \frac{3}{5}\),
suy ra \(\widehat A \approx {36^o}52';\)
\(\sin B = \frac{{20}}{{25}} = \frac{4}{5},\)
suy ra \(\widehat B \approx {53^o}8'\).
Bài 14 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc xác định các yếu tố của hàm số bậc nhất, đặc biệt là hệ số góc và ứng dụng của nó trong việc xác định mối quan hệ giữa các đường thẳng.
Bài tập yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài 14 trang 74 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử chúng ta có đường thẳng y = 2x + 1. Hệ số góc của đường thẳng này là 2. Để tìm một đường thẳng song song với đường thẳng này, chúng ta cần tìm một đường thẳng có hệ số góc bằng 2, ví dụ như y = 2x + 3.
Bài tập về hàm số bậc nhất thường xuất hiện trong các dạng sau:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, bạn nên:
Bài 14 trang 74 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập tương tự.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số góc | a, xác định độ dốc của đường thẳng |
| Đường thẳng song song | Có cùng hệ số góc |
| Bảng tóm tắt các khái niệm quan trọng | |