Bài 13 trang 109 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 13 trang 109 sách bài tập Toán 9 - Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
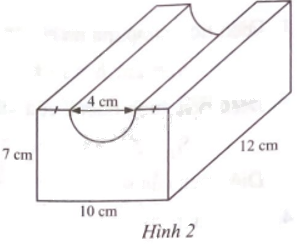
Một khối hộp chữ nhật đặc với kích thước ba cạnh là 12 cm, 10 cm, 7 cm bị khoét bởi một nửa hình trụ có đường kính 4 cm và chiều dài 12 cm (Hình 2). Tính a) Thể tích của khối còn lại b) Diện tích bề mặt của khối còn lại. (Làm tròn kết quả đến hàng đơn vị của xăngtimet khối, xăngtimet vuông).
Đề bài
Một khối hộp chữ nhật đặc với kích thước ba cạnh là 12 cm, 10 cm, 7 cm bị khoét bởi một nửa hình trụ có đường kính 4 cm và chiều dài 12 cm (Hình 2). Tính
a) Thể tích của khối còn lại
b) Diện tích bề mặt của khối còn lại.
(Làm tròn kết quả đến hàng đơn vị của xăngtimet khối, xăngtimet vuông).
Phương pháp giải - Xem chi tiết
Diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi rh\).
Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2r{\pi ^2} = 2\pi r(r + h)\).
Thể tích hình hộp chữ nhật: V = cạnh.cạnh.cạnh
Thể tích hình trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết
a) Thể tích của khối hộp chữ nhật khi chưa bị khoét là:
\({V_1} = 12.10.7 = 840\) (cm3).
Thể tích của nửa hình trụ là \({V_2} = \frac{1}{2}\pi {r^2}h = \frac{1}{2}\pi {.2^2}.12 = 24\pi \) (cm3).
Thể tích khối còn lại là: \(V = {V_1} - {V_2} = 840 - 24\pi \approx 765\)(cm3).
b) Diện tích toàn phần của khối hộp khi chưa bị khoét là:
\({S_1} = 2(7.10 + 12.10 + 7.12) = 548\) (cm2).
Diện tích xung qunah của nửa hình trụ là: \({S_2} = \pi rh = \pi .2.12 = 24\pi \)(cm2)
Diện tích hai đáy của nửa hình trụ là: \({S_3} = \pi {r^2} = 4\pi \) (cm2).
Diện tích mặt cắt dọc của nửa hình trụ là: \({S_4} = 4.12 = 48\) (cm2).
Diện tích bề mặt của khối còn lại là:
\(S = {S_1} + {S_2} - {S_3} - {S_4} = 548 + 24\pi - 4\pi - 48 \approx 563\) (cm2).
Bài 13 trang 109 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là nội dung chi tiết của bài 13:
Bài 13 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định hàm số bậc nhất biểu diễn mối quan hệ giữa hai đại lượng. Cụ thể, bài toán có thể liên quan đến:
Để giải bài toán này, học sinh cần:
(Giả sử bài toán cụ thể là về chi phí vận chuyển)
Đề bài: Một công ty vận tải tính cước phí vận chuyển hàng hóa theo công thức: Cước phí = a * Quãng đường + b (trong đó a và b là các hằng số). Biết rằng khi vận chuyển quãng đường 50km, cước phí là 150.000 đồng và khi vận chuyển quãng đường 80km, cước phí là 230.000 đồng. Hãy xác định công thức tính cước phí.
Giải:
Gọi quãng đường là x (km) và cước phí là y (đồng). Ta có hàm số y = ax + b.
Thay x = 50, y = 150.000 vào hàm số, ta được: 150.000 = 50a + b (1)
Thay x = 80, y = 230.000 vào hàm số, ta được: 230.000 = 80a + b (2)
Giải hệ phương trình (1) và (2), ta được:
Trừ (1) cho (2), ta được: -80.000 = -30a => a = 80.000/30 = 8.000/3
Thay a = 8.000/3 vào (1), ta được: 150.000 = 50 * (8.000/3) + b => b = 150.000 - 400.000/3 = 50.000/3
Vậy, công thức tính cước phí là: y = (8.000/3)x + 50.000/3
Khi giải các bài tập về hàm số bậc nhất, học sinh cần chú ý:
Để củng cố kiến thức về hàm số bậc nhất, học sinh có thể làm thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 2.
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 13 trang 109 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 và tự tin hơn trong quá trình học tập.