Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 51 sách bài tập Toán 9 - Chân trời sáng tạo tập 1. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi sắp tới.
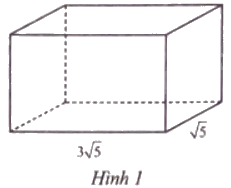
Cho hình hộp chữ nhật với chiều dài (3sqrt 5 ) cm, chiều rộng (sqrt 5 ) cm và thể tích (30sqrt 5 ) cm3 như Hình 1. Tính tổng độ dài các cạnh của hình hộp chữ nhật đó.
Đề bài
Cho hình hộp chữ nhật với chiều dài \(3\sqrt 5 \) cm, chiều rộng \(\sqrt 5 \) cm và thể tích \(30\sqrt 5 \) cm3 như Hình 1. Tính tổng độ dài các cạnh của hình hộp chữ nhật đó.
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích hình hộp chữ nhật = dài.rộng.cao để tính chiều cao.
Lời giải chi tiết
Chiều cao h = \(\frac{{30\sqrt 5 }}{{3\sqrt 5 .\sqrt 5 }} = 2\sqrt 5 \) cm.
Tổng độ dài các cạnh của hình hộp chữ nhật là \(4\left( {3\sqrt 5 + \sqrt 5 + 2\sqrt 5 } \right) = 24\sqrt 5 \) cm.
Bài 4 trang 51 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 4 bao gồm các ý nhỏ, yêu cầu học sinh:
Để giải bài 4 trang 51 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng ý nhỏ của bài 4:
Để xác định hệ số a của hàm số y = ax + b khi biết một điểm thuộc đồ thị hàm số, ta thay tọa độ của điểm đó vào phương trình hàm số và giải phương trình để tìm a.
Ví dụ: Nếu điểm A(x0; y0) thuộc đồ thị hàm số y = ax + b, thì ta có: y0 = ax0 + b. Từ đó, ta có thể giải phương trình để tìm a.
Tương tự như ý a, để tìm giá trị của b khi biết hệ số a và một điểm thuộc đồ thị hàm số, ta thay tọa độ của điểm đó và giá trị của a vào phương trình hàm số và giải phương trình để tìm b.
Ví dụ: Nếu điểm A(x0; y0) thuộc đồ thị hàm số y = ax + b và a đã biết, thì ta có: y0 = ax0 + b. Từ đó, ta có thể giải phương trình để tìm b.
Để viết phương trình đường thẳng đi qua hai điểm A(xA; yA) và B(xB; yB), ta thực hiện các bước sau:
Để xác định xem ba điểm A(xA; yA), B(xB; yB), C(xC; yC) có thẳng hàng hay không, ta sử dụng điều kiện: (yB - yA)(xC - xB) = (yC - yB)(xB - xA). Nếu điều kiện này được thỏa mãn, thì ba điểm đó thẳng hàng.
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 và các nguồn tài liệu học tập khác.
Bài 4 trang 51 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong giải quyết các bài toán thực tế. Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn trong quá trình học tập và ôn luyện.