Bài 1 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về phương trình bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải phương trình và tìm nghiệm.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chứng minh bốn đỉnh của hình vuông ABCD có cạnh bằng 16 cm đều nằm trên một đường tròn. Tính bán kính của đường tròn này.
Đề bài
Chứng minh bốn đỉnh của hình vuông ABCD có cạnh bằng 16 cm đều nằm trên một đường tròn. Tính bán kính của đường tròn này.
Phương pháp giải - Xem chi tiết
Dựa vào: Đường tròn tâm O bán kính R (R > 0) là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
Lời giải chi tiết
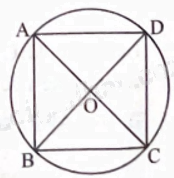
Gọi O là giao điểm của hai đường chéo của hình vuông ABCD,
Ta có OA = OB = OC = OD = \(8\sqrt 2 \) (cm), suy ra bốn đỉnh của hình vuông ABCD đều nằm trên đường tròn (O; \(8\sqrt 2 \) cm).
Bài 1 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1 thuộc chương trình học về phương trình bậc hai. Mục tiêu chính của bài tập này là giúp học sinh củng cố kiến thức về các phương pháp giải phương trình bậc hai, bao gồm phương pháp phân tích thành nhân tử, phương pháp sử dụng công thức nghiệm và phương pháp hoàn thiện bình phương.
Bài tập yêu cầu học sinh giải các phương trình bậc hai sau:
Để giải các phương trình trên, chúng ta có thể sử dụng các phương pháp sau:
x = (-b ± √(b2 - 4ac)) / 2a
Ta có thể phân tích phương trình thành nhân tử như sau:
(x - 2)(x - 3) = 0
Từ đó, ta có hai nghiệm:
Sử dụng công thức nghiệm, ta có:
a = 2, b = 7, c = 3
Δ = b2 - 4ac = 72 - 4 * 2 * 3 = 49 - 24 = 25
x = (-7 ± √25) / (2 * 2) = (-7 ± 5) / 4
Từ đó, ta có hai nghiệm:
Ta có thể viết lại phương trình như sau:
(x - 2)2 = 0
Từ đó, ta có nghiệm kép:
Ta có thể phân tích phương trình thành nhân tử như sau:
x(3x - 5) = 0
Từ đó, ta có hai nghiệm:
Bài 1 trang 84 sách bài tập Toán 9 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phương trình bậc hai. Việc nắm vững các phương pháp giải phương trình bậc hai sẽ giúp học sinh tự tin giải các bài tập tương tự và đạt kết quả tốt trong các kỳ thi.
Khi giải phương trình bậc hai, cần chú ý kiểm tra điều kiện xác định của phương trình và lựa chọn phương pháp giải phù hợp để đảm bảo tính chính xác và hiệu quả.