Giải bài 6 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2

Giải bài 6 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2

Giải bài 6 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2

Bài 6 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.

Cho hình vuông ABCD và điểm M bất kì trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với DM tại H. Chứng minh BHCD là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BHCD.

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 6 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2 1

Chứng minh tam giác BHD và tam giác BCD nội tiếp đường tròn đường kính BD. Từ đó suy ra BHCD nội tiếp đường trònđường kính BD. Suy ra I là tâm của đường tròn ngoại tiếp tứ giác BHCD.

Lời giải chi tiết

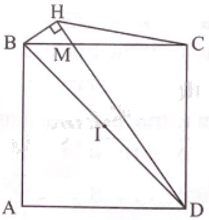
Giải bài 6 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2 2

Ta có \(\widehat {BCD} = {90^o}\)(gt); \(\widehat {BHD} = {90^o}\)(gt).

Tam giác BHD vuông tại H và tam giác BCD vuông tại C cùng nội tiếp đường tròn đường kính BD.

Do đó, tứ giác BHCD nội tiếp đường tròn đường kính BD.

Gọi I là trung điểm của BD, khi đó I là tâm của đường tròn ngoại tiếp tứ giác BHCD.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 6 trang 82 sách bài tập toán 9 - Chân trời sáng tạo tập 2 đặc sắc thuộc chuyên mục toán lớp 9 trên nền tảng toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 6 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 6 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:

Hàm số bậc nhất: Định nghĩa, dạng tổng quát y = ax + b (a ≠ 0).
Hệ số a: Xác định tính chất đồng biến, nghịch biến của hàm số.
Hệ số b: Xác định giao điểm của đồ thị hàm số với trục Oy.
Đồ thị hàm số bậc nhất: Cách vẽ đồ thị hàm số, xác định các điểm thuộc đồ thị.
Ứng dụng của hàm số bậc nhất: Giải các bài toán thực tế liên quan đến hàm số.

Lời giải chi tiết bài 6 trang 82 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2

Đề bài: (Nội dung đề bài sẽ được thay thế ở đây, ví dụ: Cho hàm số y = 2x - 3. Tìm các điểm thuộc đồ thị hàm số có hoành độ là -1, 0, 1.)

Lời giải:

Với x = -1: Thay x = -1 vào hàm số y = 2x - 3, ta được y = 2*(-1) - 3 = -5. Vậy điểm cần tìm là A(-1; -5).
Với x = 0: Thay x = 0 vào hàm số y = 2x - 3, ta được y = 2*0 - 3 = -3. Vậy điểm cần tìm là B(0; -3).
Với x = 1: Thay x = 1 vào hàm số y = 2x - 3, ta được y = 2*1 - 3 = -1. Vậy điểm cần tìm là C(1; -1).

Các dạng bài tập thường gặp và phương pháp giải

Ngoài bài tập tìm điểm thuộc đồ thị hàm số, bài 6 trang 82 và các bài tập tương tự thường gặp các dạng sau:

Xác định hệ số a, b của hàm số: Dựa vào thông tin đề bài cung cấp (ví dụ: đồ thị hàm số đi qua một điểm cho trước) để lập hệ phương trình và giải tìm a, b.
Vẽ đồ thị hàm số: Xác định hai điểm thuộc đồ thị hàm số (thường là giao điểm với trục Ox và Oy) và nối chúng lại.
Giải bài toán thực tế: Chuyển bài toán thực tế về dạng bài toán toán học, sử dụng kiến thức về hàm số bậc nhất để giải quyết.

Ví dụ minh họa thêm

Ví dụ: Tìm giá trị của x để hàm số y = -x + 2 có giá trị bằng 0.

Lời giải:

Để hàm số y = -x + 2 có giá trị bằng 0, ta cần giải phương trình -x + 2 = 0. Giải phương trình, ta được x = 2.

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.

Tổng kết

Bài 6 trang 82 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Việc nắm vững kiến thức lý thuyết và luyện tập thường xuyên sẽ giúp các em học sinh giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.