Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 8 trang 69 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Bạn Minh quan tâm đến mối liên hệ giữa giới tính và màu sắc yêu thích nhất của mỗi người. Sau khi phỏng vấn tất cả 40 học sinh lớp 9A, Minh thu được kết quả sau: Chọn ngẫu nhiên 1 bạn trong lớp 9A. Tính xác suất của biến cố sau: A: “Bạn được chọn là nam và yêu thích nhất màu đen”; B: “Bạn được chọn yêu thích nhất màu xanh”; C: “Bạn được chọn yêu thích nhất màu xanh hoặc màu đỏ”; D: “Bạn được chọn là nữ và có màu sắc yêu thích nhất không phải là màu đỏ”.
Đề bài
Bạn Minh quan tâm đến mối liên hệ giữa giới tính và màu sắc yêu thích nhất của mỗi người. Sau khi phỏng vấn tất cả 40 học sinh lớp 9A, Minh thu được kết quả sau:
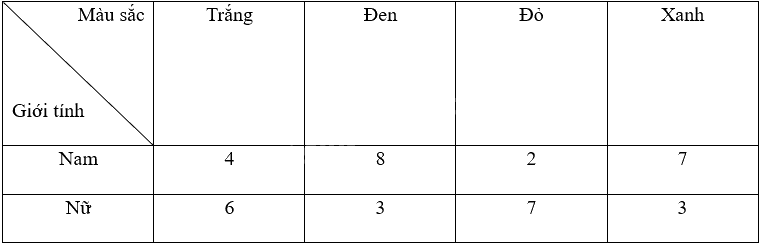
Chọn ngẫu nhiên 1 bạn trong lớp 9A. Tính xác suất của biến cố sau:
A: “Bạn được chọn là nam và yêu thích nhất màu đen”;
B: “Bạn được chọn yêu thích nhất màu xanh”;
C: “Bạn được chọn yêu thích nhất màu xanh hoặc màu đỏ”;
D: “Bạn được chọn là nữ và có màu sắc yêu thích nhất không phải là màu đỏ”.
Phương pháp giải - Xem chi tiết
Không gian mẫu là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
Một kết quả có thể của T để biến cố E xảy ra được gọi là kết quả thuận lợi cho biến cố E.
Trong phép thử ngẫu nhiên, hai kết quả đồng khả năng nếu chúng có khả năng xảy ra như nhau.
Xác suất của biến cố A được tính bởi công thức:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}}\), trong đó n(A) là số kết quả thuận lợi cho A; \(n(\Omega )\) là số các kết quả có thể xảy ra.
Lời giải chi tiết
Do lớp 9A có 40 học sinh nên số kết quả có thể xảy ra của phép thử là \(n\left( \Omega \right) = 40\).
Số kết quả thuận lợi cho biến cố A là n(A) = 8. Xác suất của biến cố A là P(A) = \(\frac{8}{{40}} = 0,2\).
Số học sinh yêu thích nhất màu xanh là 7 + 3 = 10 (học sinh). Số kết quả thuận lợi cho biến cố B là n(B) = 10. Xác suất của biến cố B là P(B) = \(\frac{{10}}{{40}} = 0,25\).
Số học sinh yêu thích nhất màu xanh hoặc màu đỏ là 7 + 3 + 2 + 7 = 19 (học sinh). Số kết quả thuận lợi cho biến cố C là n(C) = 19. Xác suất của biế cố C là P(C) = \(\frac{{19}}{{40}} = 0,475\).
Số học sinh nữ có màu sắc yêu thích nhất không phải là màu đỏ là 6 + 3 + 3 = 12 (học sinh). Số kết quả thuận lợi cho biến cố D là n(D) = 12. Xác suất của biến cố D là P(D) = \(\frac{{12}}{{40}} = 0,3\).
Bài 8 trang 69 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước.
Bài 8 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 8 trang 69 sách bài tập Toán 9 - Chân trời sáng tạo tập 2, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 8 trang 69 sách bài tập Toán 9 - Chân trời sáng tạo tập 2:
Giả sử hàm số y = ax + b đi qua điểm A(x0; y0). Thay x = x0 và y = y0 vào phương trình hàm số, ta được: y0 = ax0 + b. Từ đó, ta có thể giải phương trình để tìm ra giá trị của a.
Sau khi đã tìm được giá trị của a, ta thay a và x0, y0 vào phương trình y0 = ax0 + b để tìm ra giá trị của b.
Để viết phương trình đường thẳng đi qua hai điểm A(x1; y1) và B(x2; y2), ta thực hiện các bước sau:
Để kiểm tra xem một điểm C(xc; yc) có thuộc đồ thị hàm số y = ax + b hay không, ta thay x = xc vào phương trình hàm số và tính giá trị của y. Nếu giá trị y tính được bằng yc thì điểm C thuộc đồ thị hàm số, ngược lại thì không.
Ví dụ: Cho hàm số y = 2x - 1. Kiểm tra xem điểm A(1; 1) có thuộc đồ thị hàm số hay không.
Thay x = 1 vào phương trình hàm số, ta được: y = 2 * 1 - 1 = 1. Vì giá trị y tính được bằng tung độ của điểm A, nên điểm A thuộc đồ thị hàm số.
Để củng cố kiến thức về hàm số bậc nhất, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 2 hoặc trên các trang web học toán online.
Bài 8 trang 69 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và cách vận dụng kiến thức vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và những lưu ý trên, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả.