Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 7 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp đáp án, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho đồ thị của các hàm số y = ax2 (a( ne )0) và y = a’x2 (a’( ne )0) (Hình 4). Cho biết điểm A thuộc đồ thị của hàm số y = ax2, điểm B thuộc đồ thị của hàm số y = a’x2. a) Xác định các hệ số a và a’ b) Lấy điểm A’ đối xứng với A qua trục tung. Điểm A’ có thuộc đồ thị hàm số y = ax2 không? Vì sao? c) Biết rằng điểm M(4; b) thuộc đồ thị của hàm số y = a’x2, hãy tính b. Điểm M’ (- 4; b) có thuộc đồ thị của hàm số y = a’x2 không? Vì sao?
Đề bài
Cho đồ thị của các hàm số y = ax2 (a \( \ne \) 0) và y = a’x2 (a’ \( \ne \) 0) (Hình 4).
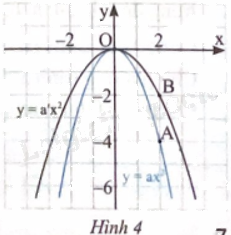
Cho biết điểm A thuộc đồ thị của hàm số y = ax2, điểm B thuộc đồ thị của hàm số y = a’x2.
a) Xác định các hệ số a và a’
b) Lấy điểm A’ đối xứng với A qua trục tung. Điểm A’ có thuộc đồ thị hàm số y = ax2 không? Vì sao?
c) Biết rằng điểm M(4; b) thuộc đồ thị của hàm số y = a’x2, hãy tính b. Điểm M’ (- 4; b) có thuộc đồ thị của hàm số y = a’x2 không? Vì sao?
Phương pháp giải - Xem chi tiết
Nhìn đồ thị xác định điểm A, B thay lần lượt vào y = ax2 và y = a’x2 để tìm a và a’..
Xác định điểm A’, M’ rồi kiểm tra có thuộc y = ax2 và y = a’x2 rồi kết luận.
Lời giải chi tiết
a) Thay toạ độ điểm A(2; - 4) vào y = ax2 , ta tìm được a = - 1. Vậy (P): y = - x2.
Thay toạ độ điểm B(2; -2) vào y = a’x2 , ta tìm được a’ = \( - \frac{1}{2}\). Vậy (P): y = \( - \frac{1}{2}\)x2.
b) Điểm A’ đối xứng với điểm A qua trục tung nên A’(- 2; 4). Do đó điểm A’(- 2; - 4) cũng thuộc (P).
c) Thay toạ độ điểm M(4; b) vào y = \( - \frac{1}{2}\)x2 , ta tìm được b = -8. Suy ra M(4; - 8). Điểm M’(-4; -8) đối xứng với điểm M qua trục tung, do đó M’ thuộc (P’).
Bài 6 trang 7 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số, và cách xác định phương trình đường thẳng.
Bài 6 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b, trong đó a là hệ số góc.
Ví dụ: Cho đường thẳng 2x + 3y = 6. Ta có thể viết lại phương trình này như sau:
3y = -2x + 6
y = (-2/3)x + 2
Vậy hệ số góc của đường thẳng là -2/3.
Để tìm giao điểm của hai đường thẳng, ta cần giải hệ phương trình gồm phương trình của hai đường thẳng đó.
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Ta có hệ phương trình:
y = x + 1
y = -x + 3
Thay y = x + 1 vào phương trình thứ hai, ta được:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình y = x + 1, ta được:
y = 1 + 1 = 2
Vậy giao điểm của hai đường thẳng là (1, 2).
Để vẽ đồ thị hàm số, ta cần xác định một vài điểm thuộc đồ thị hàm số đó. Sau đó, ta nối các điểm này lại với nhau để được đồ thị hàm số.
Ví dụ: Vẽ đồ thị hàm số y = 2x - 1.
Ta có thể xác định một vài điểm thuộc đồ thị hàm số như sau:
Nối các điểm (0, -1), (1, 1), (2, 3) lại với nhau, ta được đồ thị hàm số y = 2x - 1.
Khi giải bài tập về hàm số, các em cần lưu ý những điều sau:
Để củng cố kiến thức về hàm số, các em có thể làm thêm một số bài tập tương tự như:
Hy vọng rằng bài viết này đã giúp các em hiểu rõ hơn về cách giải bài 6 trang 7 Sách bài tập Toán 9 - Chân trời sáng tạo tập 2. Chúc các em học tập tốt!