Bài 2 trang 99 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số, tìm đỉnh của parabol và vẽ đồ thị hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tính diện tích xung quanh và thể tích của mỗi hình trụ sau:
Đề bài
Tính diện tích xung quanh và thể tích của mỗi hình trụ sau:
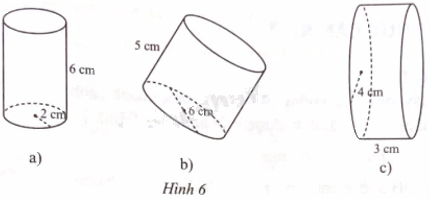
Phương pháp giải - Xem chi tiết
Diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi rh\).
Thể tích hình trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết
a) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2.\pi .2.6 = 24\pi \)(cm2).
Thể tích hình trụ là:
\(V = \pi {r^2}h = \pi {.2^2}.6 = 24\pi \)(cm3).
b) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2.\pi .3.5 = 30\pi \)(cm2).
Thể tích hình trụ là:
\(V = \pi {r^2}h = \pi {.3^2}.5 = 45\pi \)(cm3).
c) Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2.\pi .4.3 = 24\pi \)(cm2).
Thể tích hình trụ là:
\(V = \pi {r^2}h = \pi {.4^2}.3 = 48\pi \)(cm3).
Bài 2 trang 99 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Trước khi bắt đầu giải bài tập, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập sẽ yêu cầu:
Sau khi xác định rõ yêu cầu, chúng ta có thể bắt đầu giải bài tập theo các bước sau:
(Giả sử đề bài cụ thể của bài 2 trang 99 là: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.)
Giải:
Hàm số y = x2 - 4x + 3 có a = 1, b = -4, c = 3.
Tọa độ đỉnh của parabol là:
x0 = -b/2a = -(-4)/(2*1) = 2
y0 = f(x0) = f(2) = 22 - 4*2 + 3 = 4 - 8 + 3 = -1
Vậy, tọa độ đỉnh của parabol là I(2, -1).
Để vẽ đồ thị hàm số, chúng ta lập bảng giá trị:
| x | y |
|---|---|
| 0 | 3 |
| 1 | 0 |
| 2 | -1 |
| 3 | 0 |
| 4 | 3 |
Vẽ đồ thị hàm số y = x2 - 4x + 3 dựa trên bảng giá trị.
Khi giải bài tập về hàm số bậc hai, bạn cần lưu ý những điều sau:
Bài 2 trang 99 sách bài tập Toán 9 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc hai. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải bài tập và nắm vững kiến thức về hàm số bậc hai.