Bài 17 trang 54 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về phương trình bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 17 trang 54, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
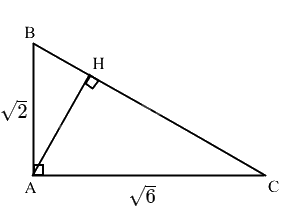
Cho tam giác ABC vuông tại A, (AB = sqrt 2 ,AC = sqrt 6 ). Tính giá trị đúng (không làm trò) của a) Chu vi và diện tích tam giác ABC. b) Độ dài đường cao AH của tam giác ABC.
Đề bài
Cho tam giác ABC vuông tại A, \(AB = \sqrt 2 ,AC = \sqrt 6 \). Tính giá trị đúng (không làm trò) của
a) Chu vi và diện tích tam giác ABC.
b) Độ dài đường cao AH của tam giác ABC.
Phương pháp giải - Xem chi tiết
Dựa vào công thức chu vi tam giác ABC: \(P = AB + AC + BC;\)
diện tích tam giác ABC: \(S = \frac{1}{2}AB.AC\) .
Lời giải chi tiết
a) \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {2 + 6} = \sqrt 8 = 2\sqrt 2 .\)
Chu vi tam giác ABC là:
\(P = AB + AC + BC \\= \sqrt 2 + \sqrt 6 + 2\sqrt 2 = \sqrt 6 + 3\sqrt 2 .\)
Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC = \frac{1}{2}.\sqrt 2 .\sqrt 6 = \sqrt 3 \).
b) Ta có \(S = \frac{1}{2}BC.AH\)
suy ra \(AH = \frac{{2S}}{{BC}} = \frac{{2\sqrt 3 }}{{2\sqrt 2 }} = \frac{{\sqrt 6 }}{2}\).
Bài 17 trang 54 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 thuộc chương trình học về phương trình bậc hai. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để giải bài 17 trang 54 sách bài tập Toán 9 - Chân trời sáng tạo tập 1, chúng ta cần phân tích đề bài và lựa chọn phương pháp giải phù hợp. Dưới đây là hướng dẫn chi tiết cho từng phần của bài tập:
Phương trình được đưa ra là một phương trình bậc hai. Chúng ta có thể sử dụng công thức nghiệm để tìm ra các nghiệm của phương trình. Cụ thể:
Sau khi tính toán, chúng ta sẽ thu được các nghiệm của phương trình.
Trong phần này, chúng ta cần tìm giá trị của tham số m sao cho phương trình có nghiệm hoặc có nghiệm thỏa mãn một điều kiện nào đó. Để làm điều này, chúng ta cần sử dụng các kiến thức về delta và định lý Viète.
Ví dụ, nếu đề bài yêu cầu phương trình có hai nghiệm phân biệt, chúng ta cần đảm bảo Δ > 0. Nếu đề bài yêu cầu phương trình có nghiệm dương, chúng ta cần đảm bảo tổng và tích của các nghiệm đều dương.
Giả sử phương trình là 2x2 - 5x + 2 = 0. Chúng ta sẽ giải phương trình này như sau:
Δ = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Để củng cố kiến thức và kỹ năng giải bài tập về phương trình bậc hai, các em học sinh có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 9 - Chân trời sáng tạo tập 1 và các tài liệu tham khảo khác.
Bài 17 trang 54 sách bài tập Toán 9 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Bằng cách nắm vững lý thuyết và phương pháp giải, các em học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Phương trình bậc hai | ax2 + bx + c = 0 (a ≠ 0) |
| Delta (Δ) | b2 - 4ac |
| Định lý Viète | x1 + x2 = -b/a, x1 * x2 = c/a |