Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
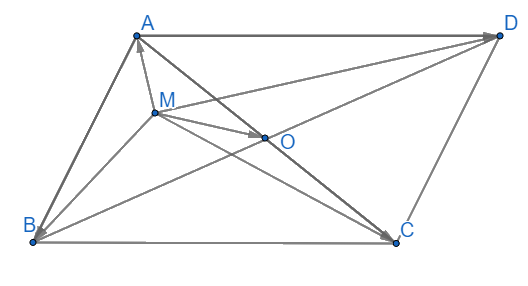
Cho hình bình hành ABCD D có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
Đề bài
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
b) \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AC} \)
Phương pháp giải - Xem chi tiết
a) Sử dụng quy tắc ba điểm \(\overrightarrow {MA} = \overrightarrow {MO} + \overrightarrow {OA} \) và tính chất trung điểm \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \)
b) Sử dụng tính chất của bình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Lời giải chi tiết
a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
\( \Leftrightarrow \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} = 4\overrightarrow {MO} \)
\( \Leftrightarrow 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO} \)
\( \Leftrightarrow 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO} = 4\overrightarrow {MO} \) (luôn đúng)
(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)
b) ABCD là hình bình hành nên ta có \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Suy ra \(\)\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC} \) (đpcm)
Bài 1 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh xác định các tập hợp, tìm phần tử thuộc tập hợp, thực hiện các phép hợp, giao, hiệu, bù của các tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 1 thường bao gồm các câu hỏi sau:
Để giải bài 1 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Bài 1: Cho các tập hợp A = {1; 2; 3; 4}, B = {3; 4; 5; 6}, C = {5; 6; 7; 8}. Hãy tìm:
Lời giải:
Ví dụ: Cho A = {a; b; c} và B = {b; c; d}. Tìm A ∪ B, A ∩ B, A \ B, B \ A.
Bài tập: Cho A = {1; 3; 5; 7} và B = {2; 4; 6; 8}. Tìm A ∪ B, A ∩ B, A \ B, B \ A.
Kiến thức về tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học khác, như lý thuyết xác suất, logic học, khoa học máy tính, và thống kê. Việc nắm vững kiến thức về tập hợp là nền tảng quan trọng để học tốt các môn học khác và giải quyết các vấn đề thực tế.
Bài 1 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 10. Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải quyết các bài tập về tập hợp và đạt kết quả tốt nhất trong môn Toán.