Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 91, 92 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học toán online hiệu quả, đồng thời cung cấp nguồn tài liệu học tập chất lượng cao, đáp ứng nhu cầu học tập của các em.
Tìm hợp lực của hai lực đối nhau Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} ;\)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\).
Phương pháp giải:
Bước 1: Thay thế vectơ bằng nhau rồi tìm tổng.
Bước 2: Tìm độ dài vectơ vừa tìm đc, độ dài vectơ \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right| = AB\).
Lời giải chi tiết:
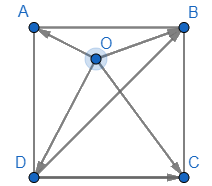
Ta có: \(AB = BC = CD = DA = 1;\)
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {DO} = \left( {\overrightarrow {DO} + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\)
\( = \left( {\overrightarrow {OC} + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)
Chú ý khi giải:
Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại
Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)
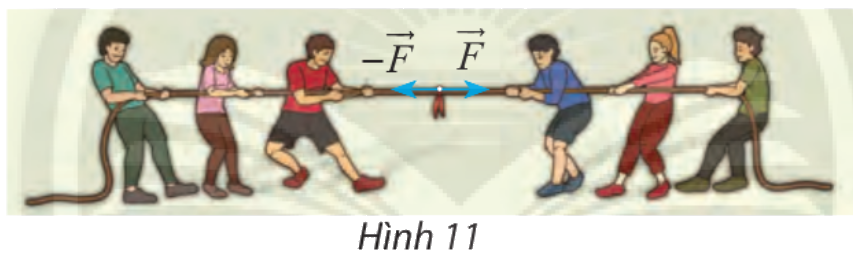
Lời giải chi tiết:
\( \overrightarrow F + \left( { - \overrightarrow F } \right) =\overrightarrow F - \overrightarrow F = \overrightarrow 0 \)
Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} ;\)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\).
Phương pháp giải:
Bước 1: Thay thế vectơ bằng nhau rồi tìm tổng.
Bước 2: Tìm độ dài vectơ vừa tìm đc, độ dài vectơ \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right| = AB\).
Lời giải chi tiết:
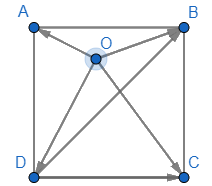
Ta có: \(AB = BC = CD = DA = 1;\)
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {DO} = \left( {\overrightarrow {DO} + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\)
\( = \left( {\overrightarrow {OC} + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)
Chú ý khi giải:
Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại
Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)
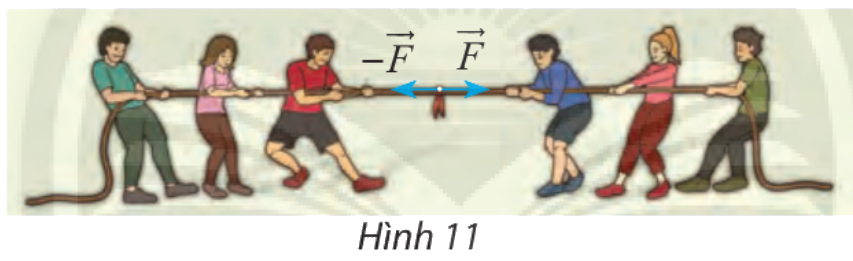
Lời giải chi tiết:
\( \overrightarrow F + \left( { - \overrightarrow F } \right) =\overrightarrow F - \overrightarrow F = \overrightarrow 0 \)
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Cụ thể, các bài tập trong mục này thường xoay quanh việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực) và sử dụng vectơ để chứng minh các tính chất hình học.
Bài tập này yêu cầu học sinh xác định tọa độ của vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ: Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ là (xB - xA, yB - yA).
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ vectơ và nhân vectơ với một số thực. Để giải bài tập này, học sinh cần nắm vững các quy tắc sau:
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh các tính chất hình học như chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, chứng minh một tứ giác là hình bình hành, v.v. Để giải bài tập này, học sinh cần kết hợp kiến thức về vectơ với kiến thức về hình học phẳng.
Bài tập: Cho A(1, 2), B(3, 4), C(5, 6). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Lời giải:
Ta có vectơ AB = (3 - 1, 4 - 2) = (2, 2) và vectơ AC = (5 - 1, 6 - 2) = (4, 4).
Vì vectơ AC = 2 * vectơ AB nên ba điểm A, B, C thẳng hàng.
Khi giải các bài tập về vectơ, học sinh cần chú ý đến dấu của tọa độ vectơ và các quy tắc về phép toán vectơ. Ngoài ra, việc vẽ hình minh họa sẽ giúp học sinh dễ dàng hình dung và tìm ra hướng giải.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 3 trang 91, 92 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!