Bài 4 trang 59 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp và biểu diễn tập hợp để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 59, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h. a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số. b) Vẽ đồ thị biểu diễn hàm số s theo t.
Đề bài
Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h.
a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số.
b) Vẽ đồ thị biểu diễn hàm số s theo t.
Lời giải chi tiết
a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ
Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)
Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)
Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)
Như vậy hàm số tính quãng đường s (km) sau t phút là:
\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)
b)
Với \(0 \le t \le 90\) thì \(s = 0,7t\)
Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)
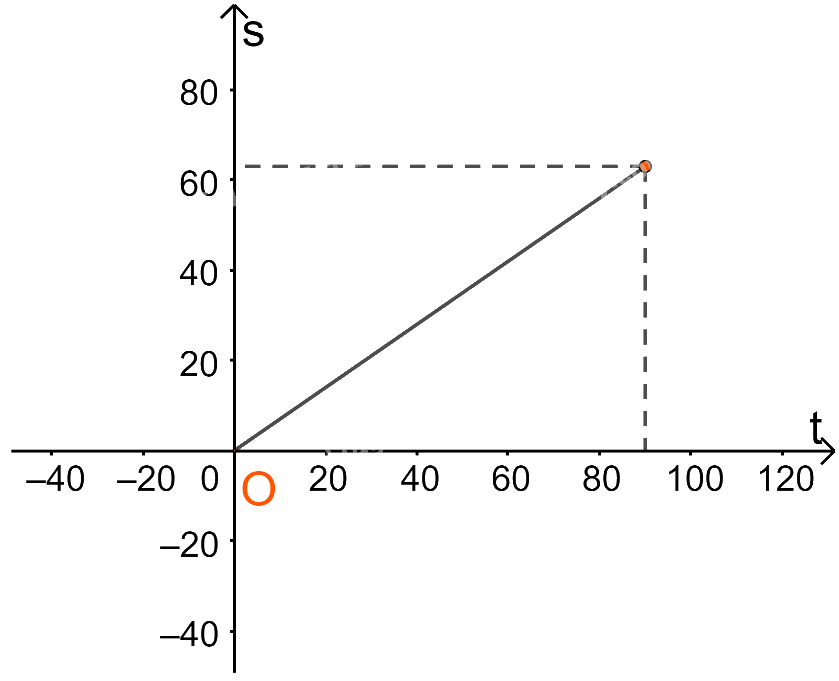
Với \(90 < t \le 105\) thì \(s = 63(km)\)
Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)
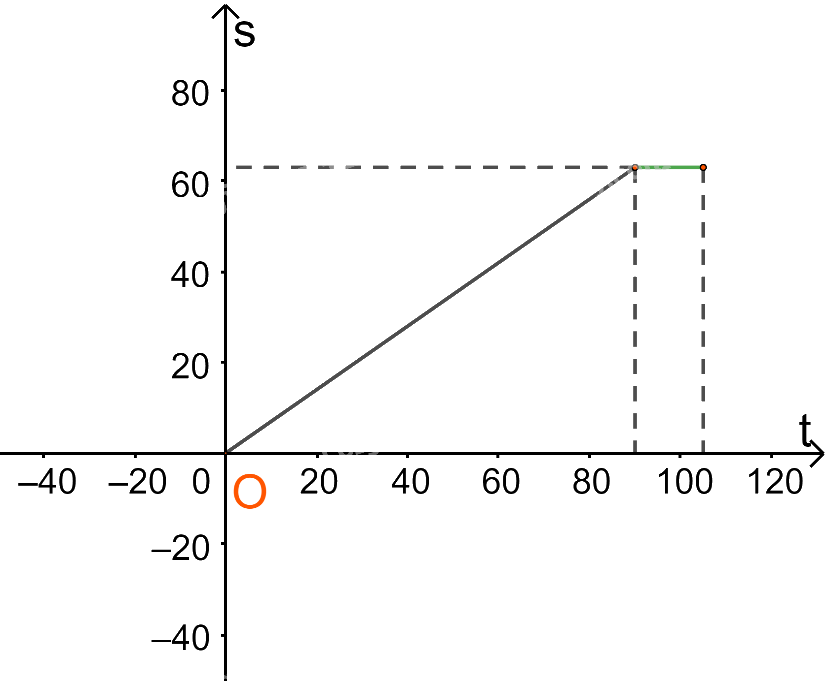
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)
Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)
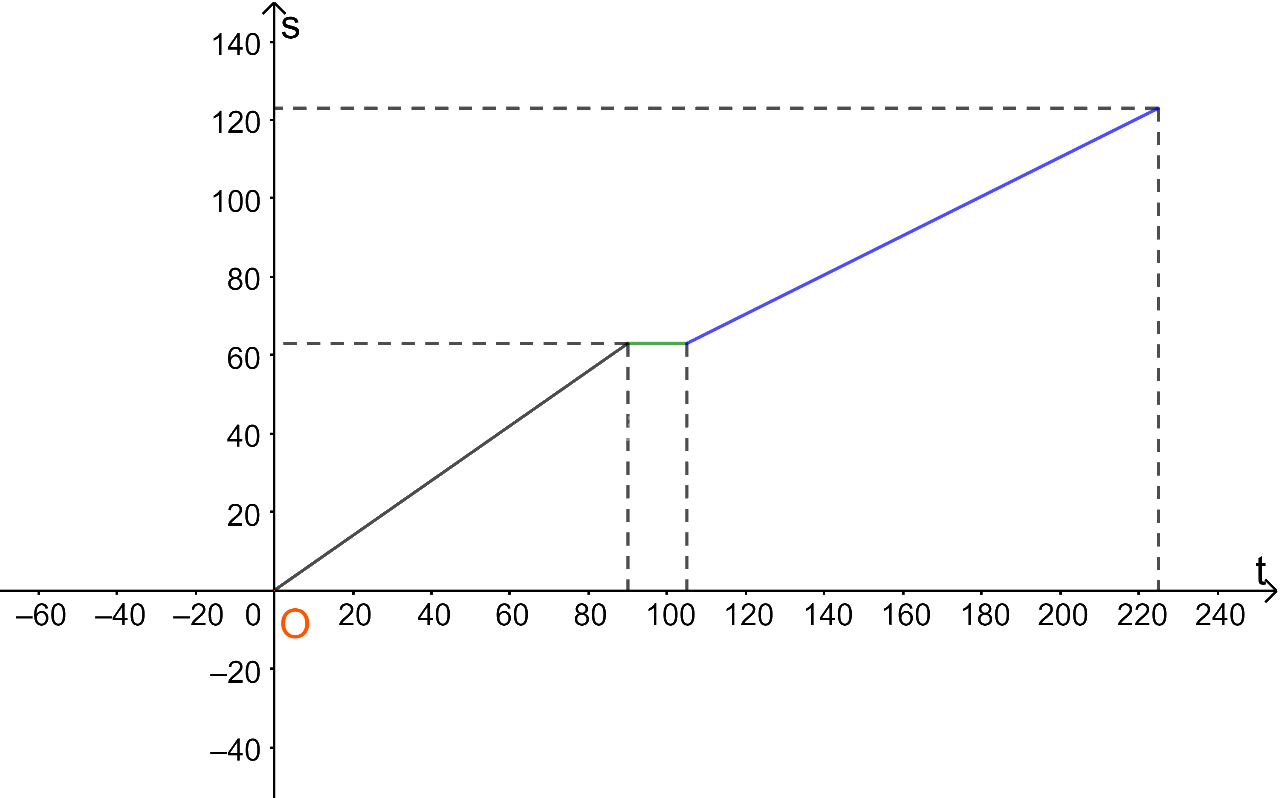
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.
Bài 4 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 4 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 4 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
Ví dụ: Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm:
Giải:
Để giải bài tập về tập hợp một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
Kiến thức về tập hợp và các phép toán trên tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Để củng cố kiến thức, bạn có thể tự giải thêm một số bài tập tương tự như:
Bài 4 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học Toán 10.