Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 81 và 82 sách giáo khoa Toán 10 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km. Tìm điểm đầu, điểm cuối, giá và độ dài của vectơ
Tìm điểm đầu, điểm cuối, giá và độ dài của vectơ \(\overrightarrow {CH} \), \(\overrightarrow {CB} \), \(\overrightarrow {HA} \) trong ví dụ 1.
Phương pháp giải:
Vectơ \(\overrightarrow {AB} \) có điểm đầu là A, điểm cuối là B và có giá là đường thẳng AB.
Lời giải chi tiết:
Vectơ \(\overrightarrow {CH} \)có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.
Vectơ \(\overrightarrow {CB} \) có điểm đầu là C, điểm cuối là B và có giá là đường thẳng CB.
Vectơ \(\overrightarrow {HA} \) có điểm đầu là H, điểm cuối là A và có giá là đường thẳng HA.
Ta có: \(CH = \frac{1}{2}CB = 1\), \(CB = 2\), \(AH = \sqrt {A{C^2} - H{C^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \).
Suy ra: \(\left| {\overrightarrow {CH} } \right| = 1\), \(\left| {\overrightarrow {CB} } \right| = 2\), \(\left| {\overrightarrow {HA} } \right| = \sqrt 3 \).
Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.
Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Khối lượng của hàng: 500 tấn.
- Độ dịch chuyển của tàu: 500km từ A đến B.
Lời giải chi tiết:
Sự khác biệt là:
- Đơn vị đo: tấn và km.
- Khối lượng hàng là đại lượng chỉ có độ lớn (500 tấn), còn độ dịch chuyển của tàu là đại lượng có cả độ lớn (500 km) và hướng (từ A đến B).
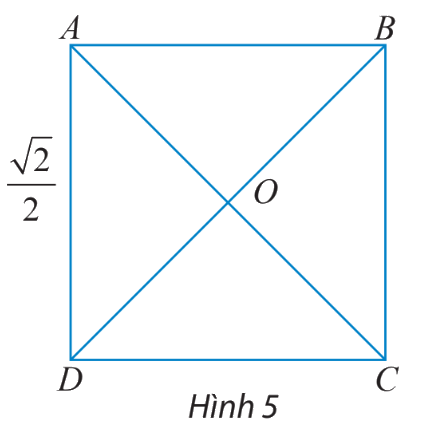
Cho hình vuông ABCD có cạnh bằng\(\frac{{\sqrt 2 }}{2}\), hai đường chéo cắt nhau tại O (hình 5). Tìm độ dài của các vectơ \(\overrightarrow {AC} ,\overrightarrow {BD} ,\overrightarrow {OA} ,\overrightarrow {AO} \).
Phương pháp giải:
Độ dài vectơ \(\overrightarrow {AC} \) là \(\left| {\overrightarrow {AC} } \right| = AC\).
Lời giải chi tiết:
Ta có: \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = 1\).
\(OA = \frac{1}{2}AC = \frac{1}{2}\).
Suy ra: \(\left| {\overrightarrow {AC} } \right| = 1\), \(\left| {\overrightarrow {BD} } \right| = 1\), \(\left| {\overrightarrow {OA} } \right| = 1\), \(\left| {\overrightarrow {AO} } \right| = 1\).
Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.
Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Khối lượng của hàng: 500 tấn.
- Độ dịch chuyển của tàu: 500km từ A đến B.
Lời giải chi tiết:
Sự khác biệt là:
- Đơn vị đo: tấn và km.
- Khối lượng hàng là đại lượng chỉ có độ lớn (500 tấn), còn độ dịch chuyển của tàu là đại lượng có cả độ lớn (500 km) và hướng (từ A đến B).
Tìm điểm đầu, điểm cuối, giá và độ dài của vectơ \(\overrightarrow {CH} \), \(\overrightarrow {CB} \), \(\overrightarrow {HA} \) trong ví dụ 1.
Phương pháp giải:
Vectơ \(\overrightarrow {AB} \) có điểm đầu là A, điểm cuối là B và có giá là đường thẳng AB.
Lời giải chi tiết:
Vectơ \(\overrightarrow {CH} \)có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.
Vectơ \(\overrightarrow {CB} \) có điểm đầu là C, điểm cuối là B và có giá là đường thẳng CB.
Vectơ \(\overrightarrow {HA} \) có điểm đầu là H, điểm cuối là A và có giá là đường thẳng HA.
Ta có: \(CH = \frac{1}{2}CB = 1\), \(CB = 2\), \(AH = \sqrt {A{C^2} - H{C^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \).
Suy ra: \(\left| {\overrightarrow {CH} } \right| = 1\), \(\left| {\overrightarrow {CB} } \right| = 2\), \(\left| {\overrightarrow {HA} } \right| = \sqrt 3 \).
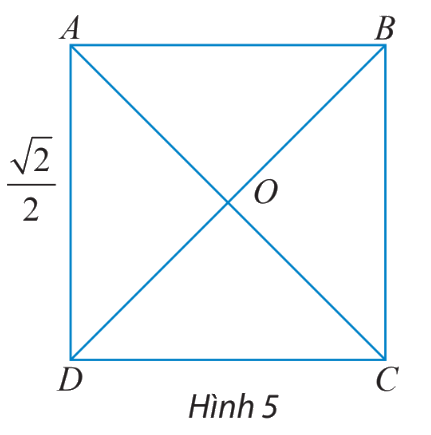
Cho hình vuông ABCD có cạnh bằng\(\frac{{\sqrt 2 }}{2}\), hai đường chéo cắt nhau tại O (hình 5). Tìm độ dài của các vectơ \(\overrightarrow {AC} ,\overrightarrow {BD} ,\overrightarrow {OA} ,\overrightarrow {AO} \).
Phương pháp giải:
Độ dài vectơ \(\overrightarrow {AC} \) là \(\left| {\overrightarrow {AC} } \right| = AC\).
Lời giải chi tiết:
Ta có: \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = 1\).
\(OA = \frac{1}{2}AC = \frac{1}{2}\).
Suy ra: \(\left| {\overrightarrow {AC} } \right| = 1\), \(\left| {\overrightarrow {BD} } \right| = 1\), \(\left| {\overrightarrow {OA} } \right| = 1\), \(\left| {\overrightarrow {AO} } \right| = 1\).
Mục 1 của chương trình Toán 10 tập 1, Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp, các phép toán trên tập hợp, và các khái niệm cơ bản về số thực. Việc nắm vững những kiến thức này là nền tảng quan trọng cho việc học tập các chương tiếp theo.
Trang 81 và 82 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các bài tập vận dụng kiến thức về tập hợp, tập con, phép hợp, giao, hiệu, phần bù của tập hợp, và các tính chất của chúng. Các bài tập được thiết kế để giúp học sinh:
Bài 1 yêu cầu học sinh liệt kê các phần tử của các tập hợp cho trước. Để giải bài này, học sinh cần nắm vững định nghĩa về tập hợp và cách xác định các phần tử của tập hợp. Ví dụ:
Cho tập hợp A = {x | x là số tự nhiên nhỏ hơn 10}. Hãy liệt kê các phần tử của tập hợp A.
Lời giải: A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Bài 2 yêu cầu học sinh xác định mối quan hệ giữa các tập hợp, ví dụ như tập con, tập bằng nhau, tập khác nhau. Để giải bài này, học sinh cần nắm vững định nghĩa về các mối quan hệ giữa các tập hợp. Ví dụ:
Cho tập hợp A = {1, 2, 3} và tập hợp B = {1, 2, 3, 4}. Hãy xác định mối quan hệ giữa A và B.
Lời giải: A là tập con của B (A ⊆ B)
Bài 3 yêu cầu học sinh thực hiện các phép toán trên tập hợp, ví dụ như phép hợp, giao, hiệu, phần bù của tập hợp. Để giải bài này, học sinh cần nắm vững các quy tắc thực hiện các phép toán trên tập hợp. Ví dụ:
Cho tập hợp A = {1, 2, 3} và tập hợp B = {2, 3, 4}. Hãy tính A ∪ B và A ∩ B.
Lời giải:
Bài 4 yêu cầu học sinh ứng dụng kiến thức về tập hợp và các phép toán trên tập hợp vào giải quyết các bài toán thực tế. Đây là loại bài tập đòi hỏi học sinh phải có khả năng phân tích và suy luận toán học. Ví dụ:
Trong một lớp học có 30 học sinh, có 15 học sinh thích môn Toán, 10 học sinh thích môn Văn, và 5 học sinh thích cả hai môn. Hỏi có bao nhiêu học sinh không thích môn Toán và không thích môn Văn?
Lời giải:
Gọi A là tập hợp các học sinh thích môn Toán, B là tập hợp các học sinh thích môn Văn.
|A| = 15, |B| = 10, |A ∩ B| = 5
Số học sinh thích ít nhất một trong hai môn là: |A ∪ B| = |A| + |B| - |A ∩ B| = 15 + 10 - 5 = 20
Số học sinh không thích môn Toán và không thích môn Văn là: 30 - 20 = 10
Hy vọng rằng với lời giải chi tiết và những lời khuyên trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 81, 82 SGK Toán 10 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!