Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 23, 24, 25 sách giáo khoa Toán 10 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
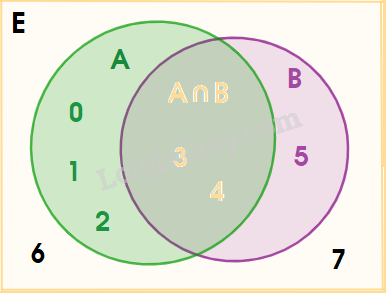
Cho tập hợp E ={ x thuộc N |x < 8} ,A = { 0;1;2;3;4} ,B = { 3;4;5} Xác định các tập hợp sau đây:
Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.
a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.
Phương pháp giải:
Viết tập hợp bằng cách liệt kê các phần tử.
Lời giải chi tiết:

a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: \(E = \{ {a_2};{a_7}\} \)
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: \(F = \{ {a_3};{a_4};{a_9}\} \)
Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)
Xác định các tập hợp sau đây:
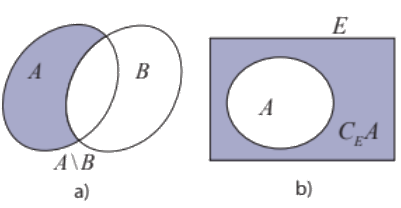
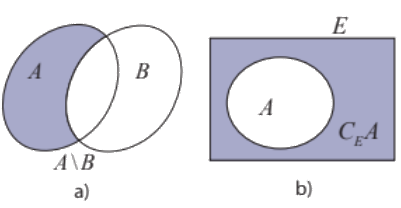
a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\)
b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\)
c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\)
Phương pháp giải:
Lời giải chi tiết:
\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
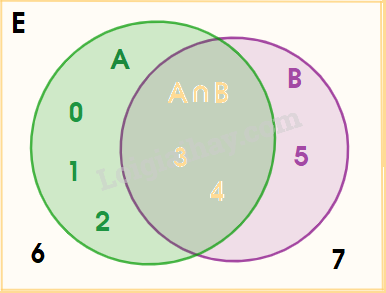
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)
Xác định các tập hợp sau đây:
a) \((1;3) \cup [ - 2;2]\)
b) \(( - \infty ;1) \cap [0;\pi ]\)
c) \([\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\)
d) \({C_\mathbb{R}}[ - 1; + \infty )\)
Phương pháp giải:
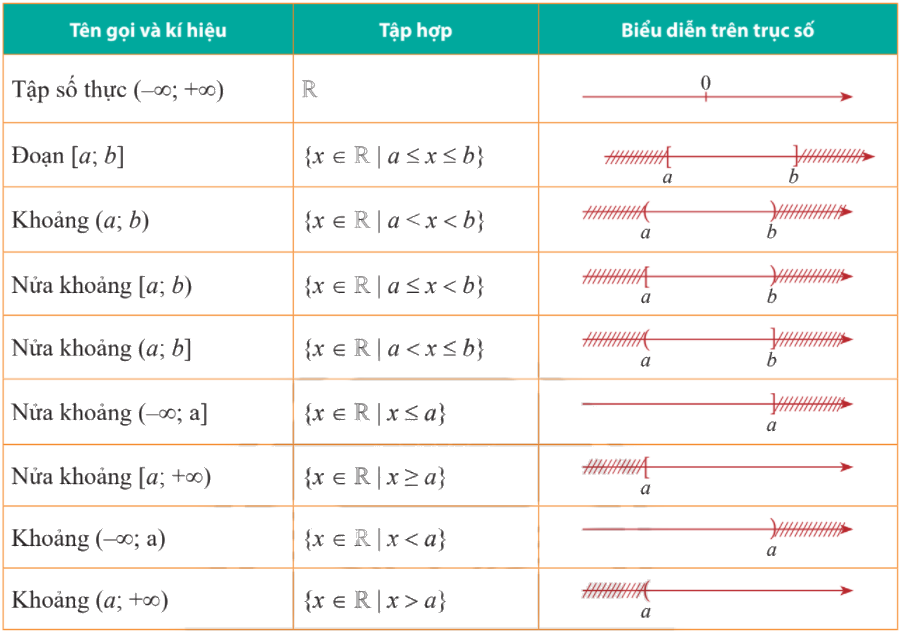
Biểu diễn các tập hợp trên trục số
Lời giải chi tiết:
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
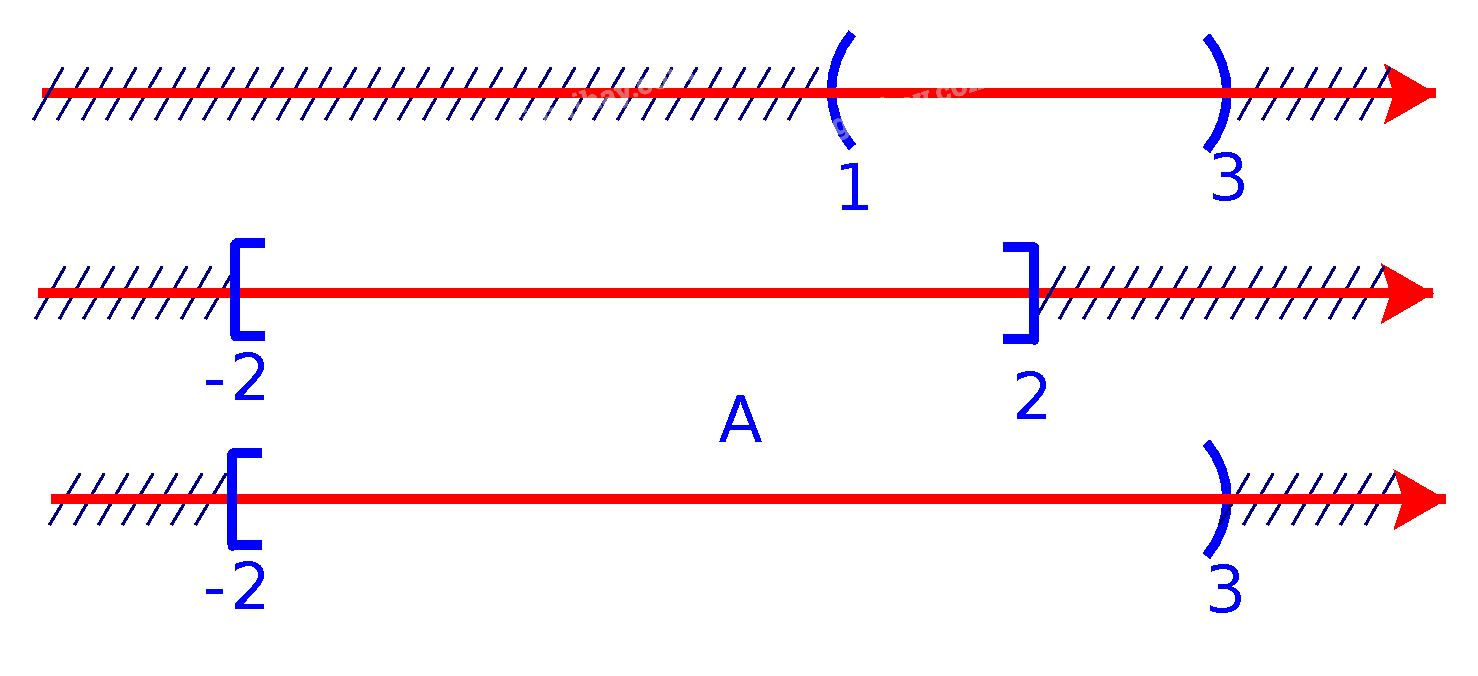
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)
b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
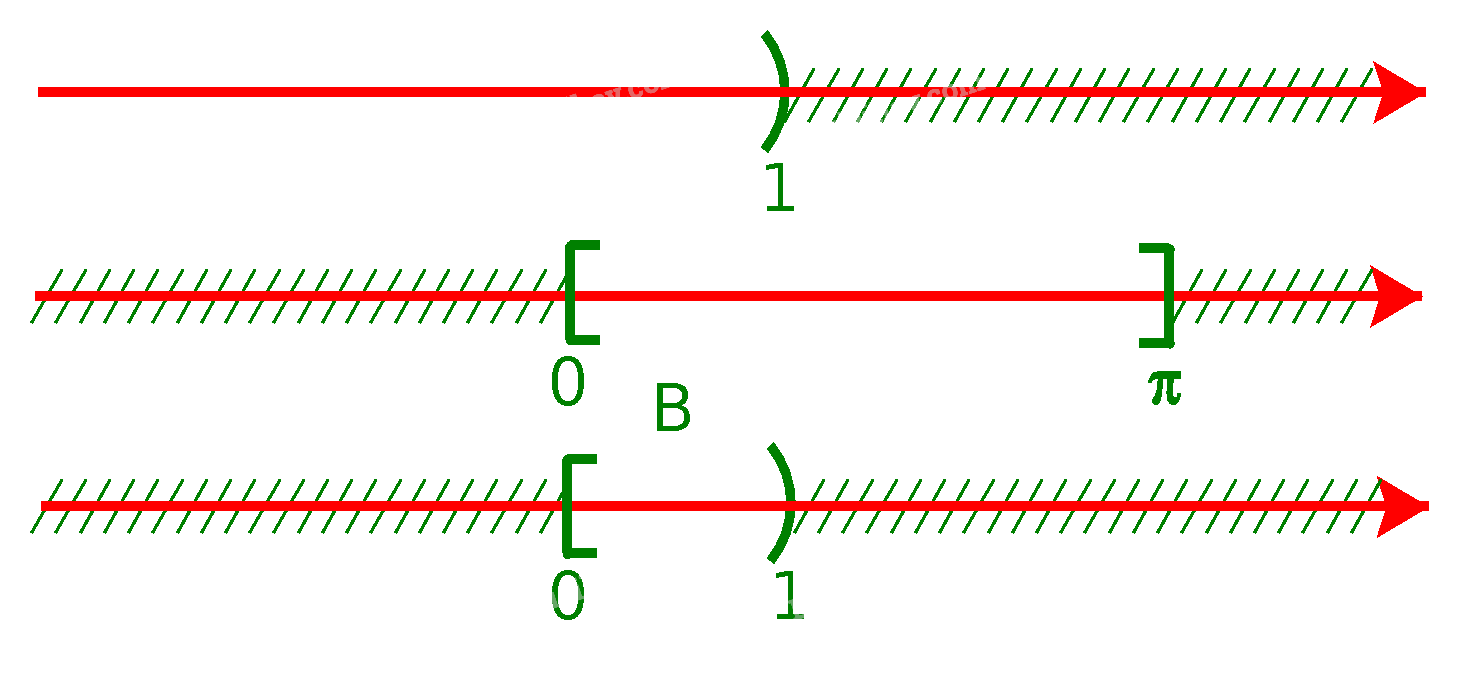
Từ sơ đồ, ta thấy \(B = [0;1)\)
c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
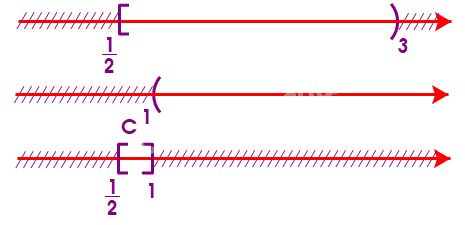
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)
d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
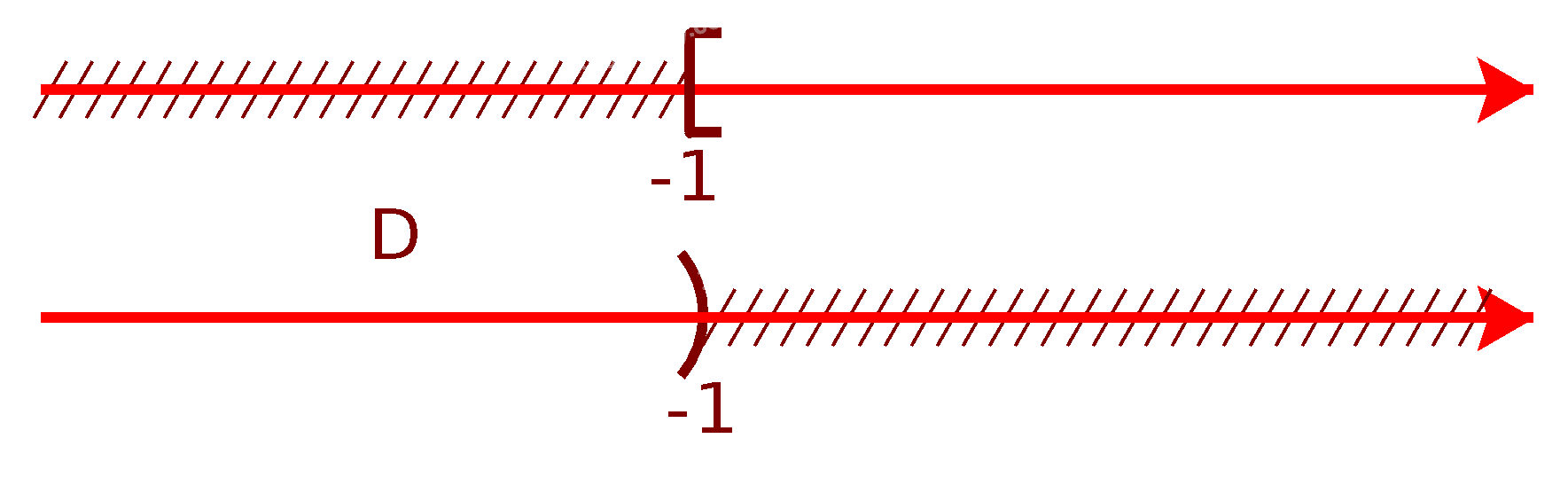
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)
Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.
a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.
Phương pháp giải:
Viết tập hợp bằng cách liệt kê các phần tử.
Lời giải chi tiết:

a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: \(E = \{ {a_2};{a_7}\} \)
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: \(F = \{ {a_3};{a_4};{a_9}\} \)
Cho tập hợp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)
Xác định các tập hợp sau đây:
a) A\B, B\A và \((A\backslash B) \cap {\rm{(}}B\backslash A)\)
b) \({C_E}(A \cap B)\) và \(({C_E}A) \cap ({C_E}B)\)
c) \({C_E}(A \cup B)\) và \(({C_E}A) \cup ({C_E}B)\)
Phương pháp giải:
Lời giải chi tiết:
\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)
Xác định các tập hợp sau đây:
a) \((1;3) \cup [ - 2;2]\)
b) \(( - \infty ;1) \cap [0;\pi ]\)
c) \([\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\)
d) \({C_\mathbb{R}}[ - 1; + \infty )\)
Phương pháp giải:
Biểu diễn các tập hợp trên trục số
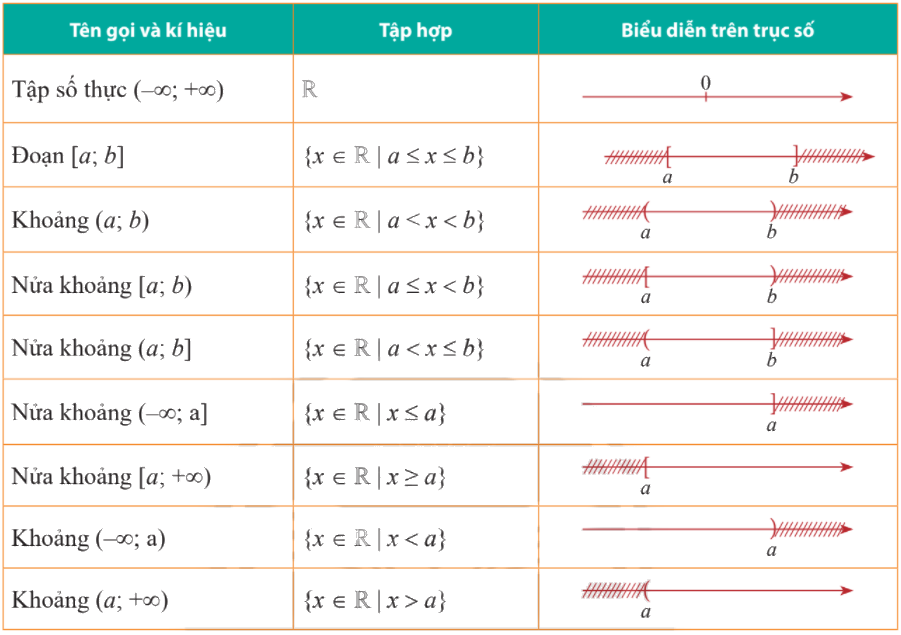
Lời giải chi tiết:
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
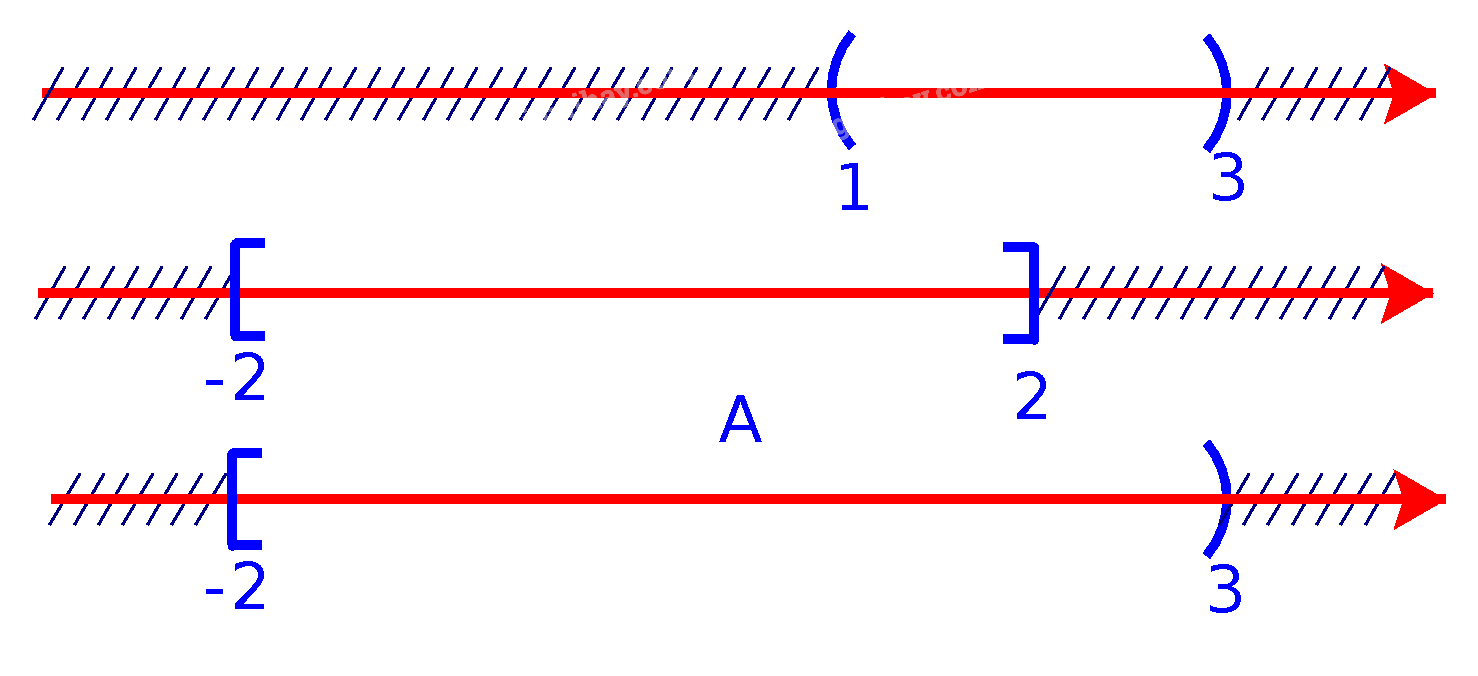
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)
b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
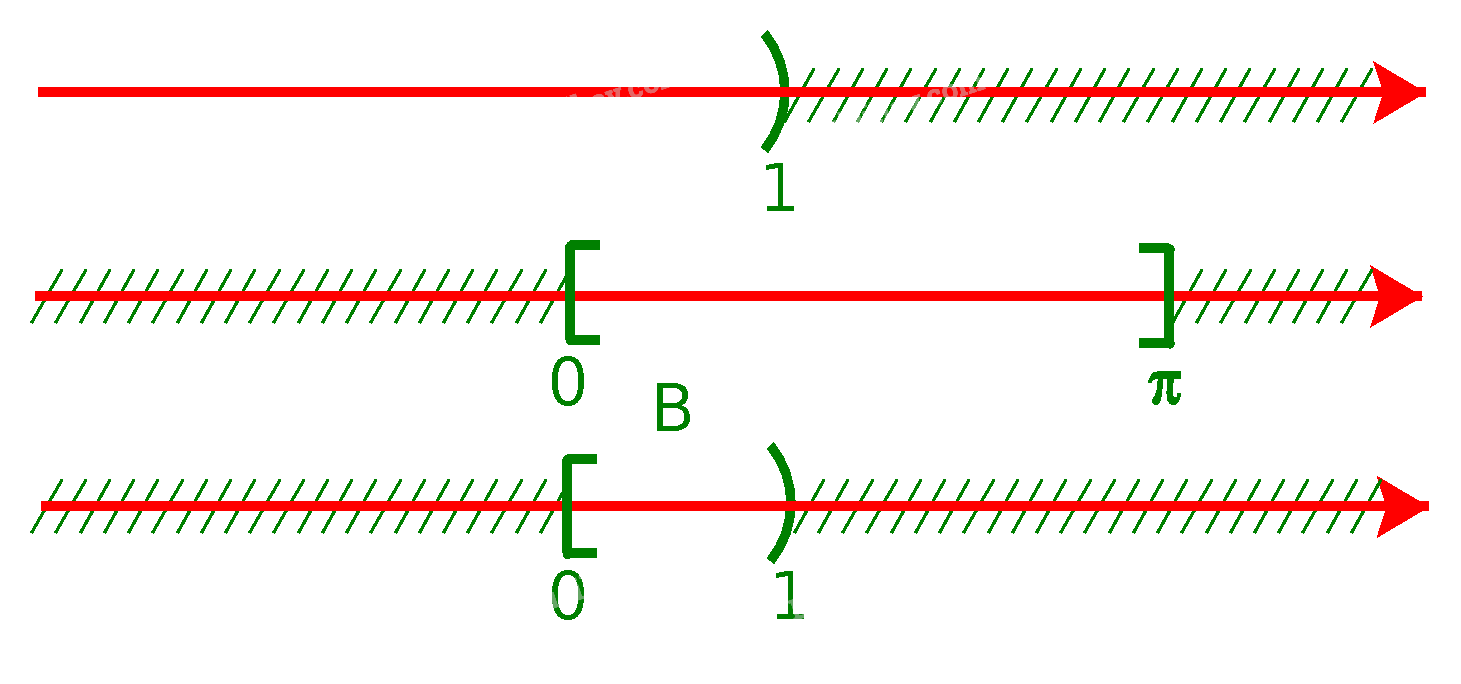
Từ sơ đồ, ta thấy \(B = [0;1)\)
c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
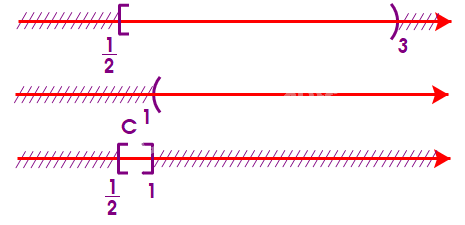
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)
d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
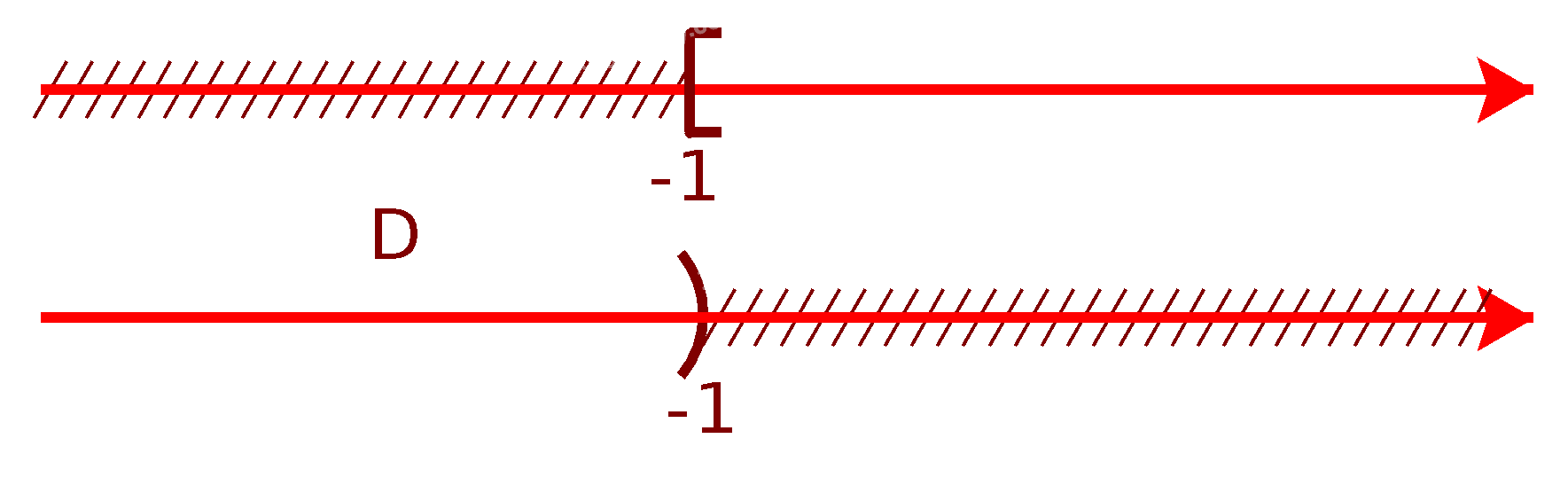
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)
Mục 2 của chương trình Toán 10 tập 1 Chân trời sáng tạo tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên. Bài viết này sẽ đi sâu vào từng bài tập trong mục 2, trang 23, 24, 25, cung cấp lời giải chi tiết, dễ hiểu, cùng với các lưu ý quan trọng để giúp các em hiểu rõ hơn về nội dung bài học.
Bài tập này yêu cầu học sinh xác định các phần tử thuộc một tập hợp cho trước. Để giải bài tập này, các em cần hiểu rõ định nghĩa của tập hợp và cách xác định các phần tử của tập hợp. Ví dụ, nếu tập hợp A chứa các số tự nhiên chẵn nhỏ hơn 10, thì các phần tử của tập hợp A là: {0, 2, 4, 6, 8}.
Bài tập này yêu cầu học sinh xác định xem một mệnh đề cho trước là đúng hay sai. Để giải bài tập này, các em cần hiểu rõ định nghĩa của mệnh đề và cách xác định tính đúng sai của mệnh đề. Ví dụ, mệnh đề “2 + 2 = 4” là một mệnh đề đúng, trong khi mệnh đề “2 + 2 = 5” là một mệnh đề sai.
Bài tập này yêu cầu học sinh thực hiện các phép toán trên tập hợp, như hợp, giao, hiệu, và phần bù. Để giải bài tập này, các em cần hiểu rõ định nghĩa của các phép toán trên tập hợp và cách thực hiện chúng. Ví dụ, nếu A = {1, 2, 3} và B = {2, 3, 4}, thì A ∪ B = {1, 2, 3, 4} và A ∩ B = {2, 3}.
Bài tập này yêu cầu học sinh chứng minh các tính chất của tập hợp, như tính giao hoán, tính kết hợp, và tính phân phối. Để giải bài tập này, các em cần hiểu rõ định nghĩa của các tính chất của tập hợp và cách chứng minh chúng. Ví dụ, tính giao hoán của phép hợp có thể được chứng minh như sau: A ∪ B = B ∪ A.
Ví dụ 1: Cho tập hợp A = {1, 2, 3, 4, 5}. Hãy tìm tập hợp B chứa các số chẵn trong A.
Lời giải: Tập hợp B chứa các số chẵn trong A là B = {2, 4}.
Ví dụ 2: Cho hai tập hợp A = {1, 2, 3} và B = {3, 4, 5}. Hãy tìm A ∪ B và A ∩ B.
Lời giải: A ∪ B = {1, 2, 3, 4, 5} và A ∩ B = {3}.
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải các bài tập trong mục 2 trang 23, 24, 25 SGK Toán 10 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!