Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
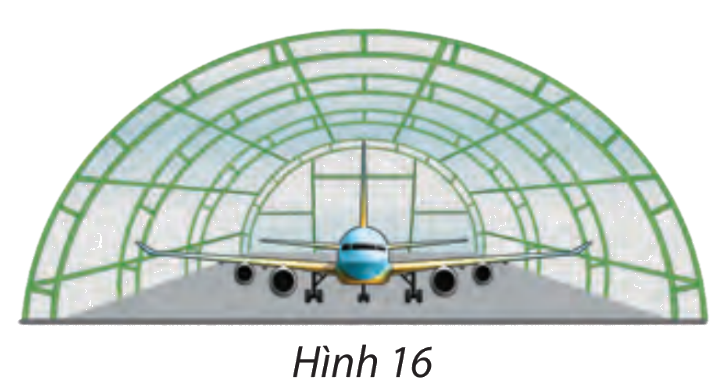
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16) a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm
Đề bài
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16)
a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên
b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm
Phương pháp giải - Xem chi tiết
a) Bước 1: Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm
Bước 2: Viết phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)
b) Bước 1: Từ dữ kiện cách chân tường 5 m, xác định cách gốc tạo độ bao nhiêu (x=?)
Bước 2: Thay x vừa tìm được vào phương trình chính tắc tìm y
Lời giải chi tiết
a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng
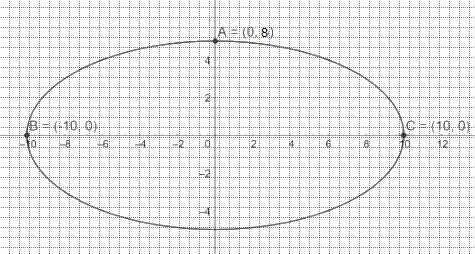
Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)
Ta có chiều cao 8 m nên \(OA = b = 8\), chiều rộng của vòm là 20 m, suy ra \(BC = 2a = 20 \Rightarrow a = 10\).
Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)
Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\), ta tìm được \(y = 4\sqrt 3 \)
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(4\sqrt 3\) m
Bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong mặt phẳng để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giải bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho từng phần của bài 4, bao gồm các bước giải, giải thích rõ ràng và dễ hiểu. Ví dụ:)
Ví dụ: Cho A(1; 2), B(3; 4). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ là (3 - 1; 4 - 2) = (2; 2).
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Bài 4 trang 71 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp bạn hiểu rõ hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với những hướng dẫn và lời giải chi tiết trên, bạn sẽ tự tin hơn trong việc giải bài tập này và đạt kết quả tốt trong môn Toán.
| Khái niệm | Định nghĩa |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Tọa độ vectơ | Cặp số (x; y) biểu diễn vectơ. |