Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 75, 76, 77 sách giáo khoa Toán 10 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên.
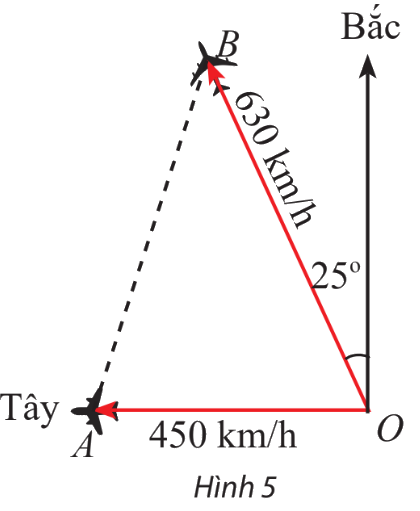
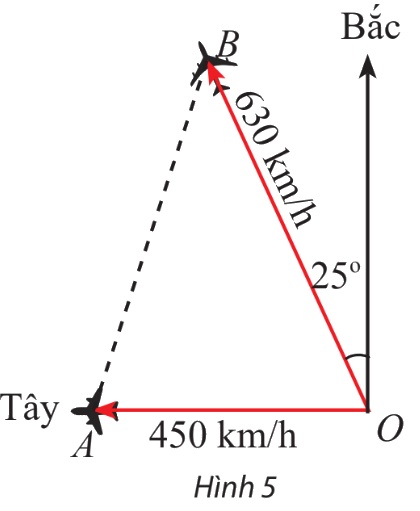
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc \({25^o}\) về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao.
Phương pháp giải:
Bước 1. Tính góc \(\widehat {BOA} = {90^o} - {25^o}.\)
Bước 2: Áp dụng định lí cosin: \(A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\)
Lời giải chi tiết:
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.
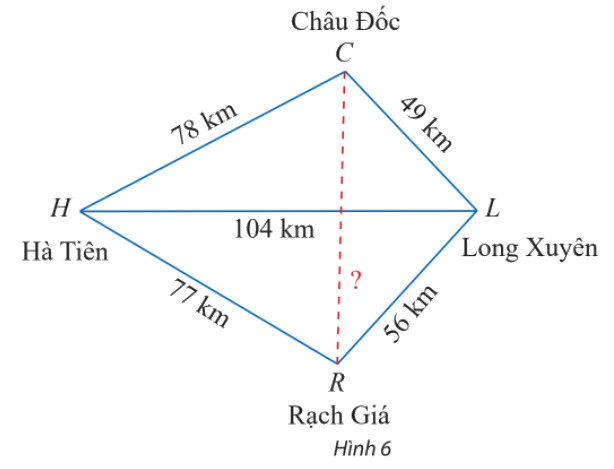
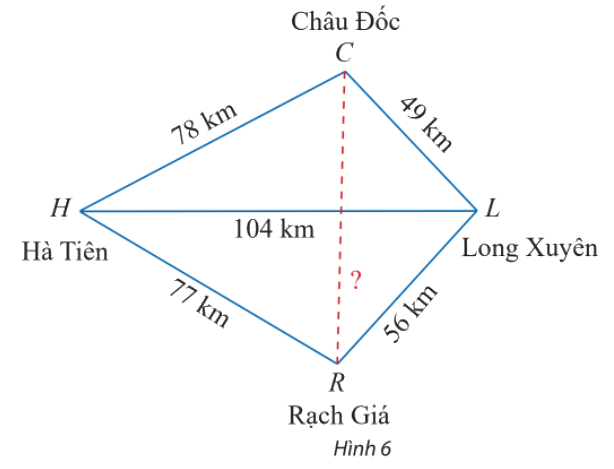
Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.
Phương pháp giải:
Bước 1: Áp dụng hệ quả của định lí cosin để tính các góc \(\widehat {CHL},\;\widehat {LHR}\)\(\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}};\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - R{L^2}}}{{2.HL.HR}}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
Lời giải chi tiết:
Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.
Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.
Phương pháp giải:
Bước 1: Áp dụng hệ quả của định lí cosin để tính các góc \(\widehat {CHL},\;\widehat {LHR}\)\(\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}};\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - R{L^2}}}{{2.HL.HR}}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
Lời giải chi tiết:
Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc \({25^o}\) về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao.
Phương pháp giải:
Bước 1. Tính góc \(\widehat {BOA} = {90^o} - {25^o}.\)
Bước 2: Áp dụng định lí cosin: \(A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\)
Lời giải chi tiết:
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.
Mục 2 của chương trình Toán 10 tập 1 Chân trời sáng tạo tập trung vào các khái niệm cơ bản về vectơ, bao gồm định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số thực), và ứng dụng của vectơ trong hình học.
Các bài tập trên trang 75 chủ yếu xoay quanh việc hiểu rõ định nghĩa vectơ, phân biệt vectơ với đoạn thẳng, và xác định các yếu tố của vectơ (điểm đầu, điểm cuối, độ dài, hướng).
Trang 76 tập trung vào việc rèn luyện kỹ năng thực hiện các phép toán cộng và trừ vectơ. Học sinh cần nắm vững quy tắc cộng và trừ vectơ, cũng như hiểu rõ ý nghĩa hình học của các phép toán này.
Trang 77 giới thiệu phép nhân vectơ với một số thực và các tính chất của phép nhân này. Học sinh cần hiểu rõ ý nghĩa của phép nhân vectơ với một số thực, cũng như cách thực hiện phép toán này.
| Bài | Nội dung |
|---|---|
| 7 | Tính tích của vectơ với một số thực. |
| 8 | Chứng minh đẳng thức vectơ liên quan đến phép nhân với một số thực. |
| 9 | Giải bài toán ứng dụng phép nhân vectơ với một số thực. |
| Lưu ý: Các bài tập có thể có nhiều cách giải khác nhau. | |
Để giải các bài tập về vectơ một cách hiệu quả, học sinh cần:
Vectơ là một công cụ mạnh mẽ trong hình học, được sử dụng để:
Để học tốt môn Toán, đặc biệt là phần vectơ, các em cần:
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 75, 76, 77 SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tốt!