Bài 12 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng chảy của nước trên con sông đó chạy với tốc độ 1,20 m/s về hướng bên phải.
Đề bài
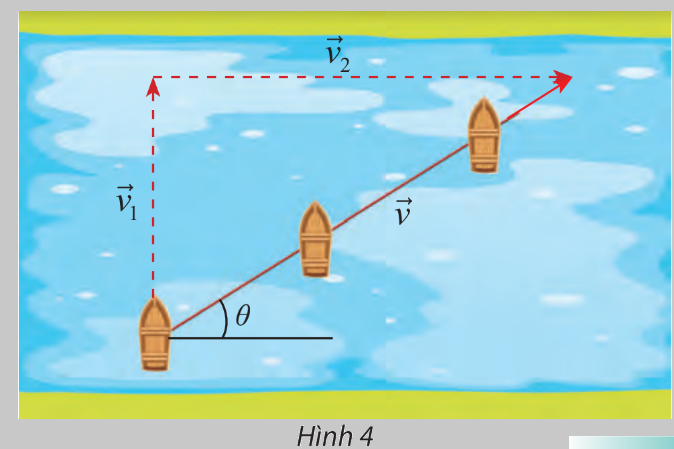
Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng chảy của nước trên con sông đó chạy với tốc độ 1,20 m/s về hướng bên phải. Gọi \(\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} ,\overrightarrow v \) lần lượt là vận tốc của thuyền so với dòng nước, vận tốc của dòng nước so với bờ và vận tốc của thuyền so với bờ.
a) Tính độ dài của các vectơ \(\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} ,\overrightarrow v \)
b) Tốc độ dịch chuyển của thuyền so với bờ là bao nhiêu?
c) Hướng di chuyển của thuyền lệch một góc bao nhiêu so với bờ?
Phương pháp giải - Xem chi tiết
a) Sử dụng tính chất trong tam giác vuông \({c^2} = {a^2} + {b^2}\) (với c là cạnh huyền của tam giác vuông và a, b là cạnh góc vuông)
b) Chỉ ra kết quả độ dài vectơ \(\overrightarrow v \) đã tính được ở câu a)
c) Sử dụng tính chất trong tam giác vuông \(\sin B = \frac{a}{c}\) (với c là cạnh huyền của tam giác vuông và a, b là cạnh góc vuông)
Lời giải chi tiết
a) Ta có:
\(\left| {\overrightarrow {{v_1}} } \right| = 0,75;\left| {\overrightarrow {{v_2}} } \right| = 1,20\)
Dựa vào hình vẽ ta thấy \(\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \) và \(\overrightarrow {{v_1}} \bot \overrightarrow {{v_2}} \)
Áp dụng tính chất trong tam giác vuông ta có: \({\left| {\overrightarrow v } \right|^2} = {\left| {\overrightarrow {{v_1}} } \right|^2} + {\left| {\overrightarrow {{v_2}} } \right|^2} \Rightarrow \left| {\overrightarrow v } \right| = \sqrt {{{\left| {\overrightarrow {{v_1}} } \right|}^2} + {{\left| {\overrightarrow {{v_2}} } \right|}^2}} = \sqrt {0,{{75}^2} + 1,{2^2}} = \frac{{3\sqrt {89} }}{{20}}\)
b) Tốc độ dịch chuyển của thuyền so với bờ là \(\frac{{3\sqrt {89} }}{{20}}\) m/s
c) Nước có hướng dichuyển song song với bờ nên hướng di chuyển của thuyền
so với bờ tương đương với hướng di chuyển của thuyền so với nước
Suy ra góc lệch giữa hướng di chuyển của thuyền và bờ là \(\left( {\overrightarrow v ,\overrightarrow {{v_2}} } \right)\)
Ta có: \(\sin \left( {\overrightarrow v ,\overrightarrow {{v_2}} } \right) = \frac{{\left| {\overrightarrow {{v_1}} } \right|}}{{\left| {\overrightarrow v } \right|}} = \frac{{0,75}}{{\frac{{3\sqrt {89} }}{{20}}}} = \frac{{5\sqrt {89} }}{{89}} \Rightarrow \left( {\overrightarrow v ,\overrightarrow {{v_2}} } \right) \simeq 32^\circ \)
Vậy hướng di chuyển của thuyền lệch một góc \(32^\circ \) so với bờ
Bài 12 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Dưới đây là đề bài và lời giải chi tiết bài 12 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo:
Đề bài: (Nội dung đề bài sẽ được điền vào đây, ví dụ: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Chứng minh rằng AM và BD cắt nhau tại một điểm.)
Lời giải:
Giải thích chi tiết từng bước:
(Giải thích chi tiết từng bước giải bài toán, bao gồm các phép tính, các bước biến đổi và các kết luận. Sử dụng các ví dụ minh họa để giúp học sinh hiểu rõ hơn.)
Lưu ý:
Bài tập tương tự:
(Liệt kê một số bài tập tương tự để học sinh luyện tập và củng cố kiến thức.)
Tổng kết:
Bài 12 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin giải quyết bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành. |