Chào mừng bạn đến với bài học lý thuyết về Giải bất phương trình bậc hai một ẩn, thuộc chương trình SGK Toán 10 Chân trời sáng tạo tại giaitoan.edu.vn.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về bất phương trình bậc hai, giúp bạn tự tin giải quyết các bài toán liên quan.
Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng
A. Lý thuyết
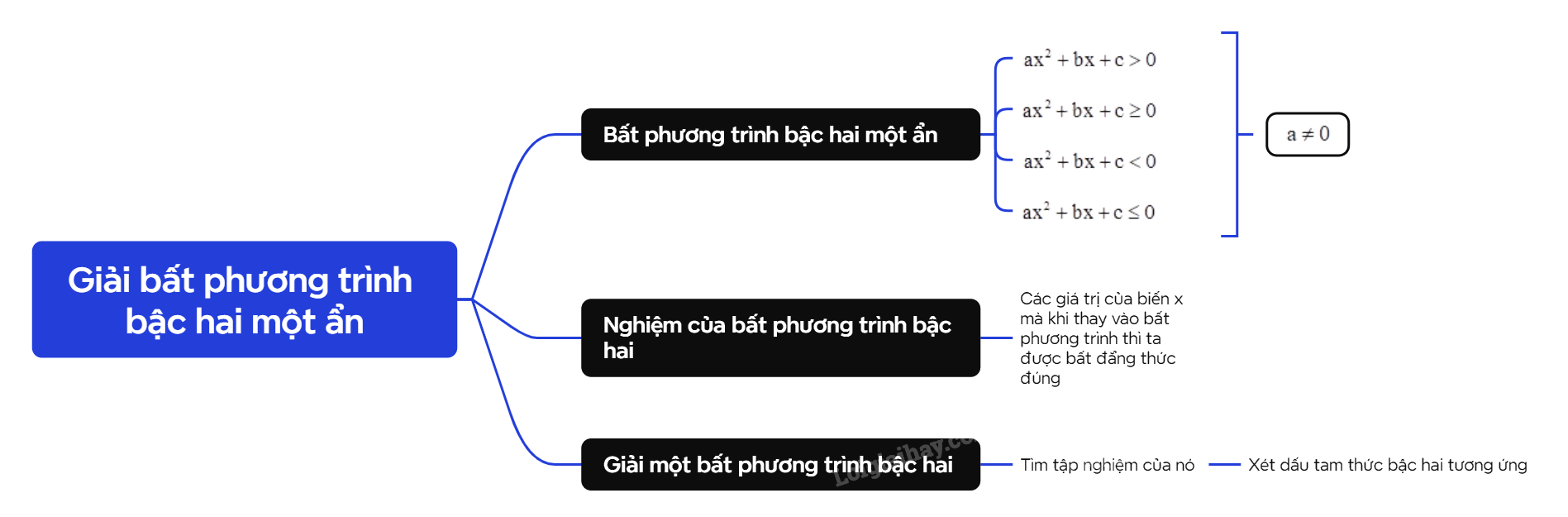
Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng \(a{x^2} + bx + c > 0\), \(a{x^2} + bx + c \ge 0\), \(a{x^2} + bx + c < 0\), \(a{x^2} + bx + c \le 0\) với \(a \ne 0\). Nghiệm của bất phương trình bậc hai là các giá trị của biến x mà khi thay vào bất phương trình thì ta được bất đẳng thức đúng. |
| Giải một bất phương trình bậc hai là tìm tập nghiệm của nó. |
Ta có thể giải bất phương trình bậc hai bằng cách xét dấu tam thức bậc hai tương ứng.
B. Bài tập
Bài 1: Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, x = 1 và x = 2 có là nghiệm của bất phương trình đó hay không?
a) \({x^2} + x - 3 \ge 0\).
b) \(3{x^3} + {x^2} - 1 \le 0\).
Giải:
a) \({x^2} + x - 3 \ge 0\) là một bất phương trình bậc hai một ẩn.
Vì \({1^2} + 1 - 3 = - 1 < 0\) nên x = 1 không là nghiệm của bất phương trình trên.
Vì \({2^2} + 2 - 3 = 3 > 0\) nên x = 2 là một nghiệm của bất phương trình trên.
b) \(3{x^3} + {x^2} - 1 \le 0\) không phải là một bất phương trình bậc hai một ẩn.
Bài 2: Giải các bất phương trình sau:
a) \(3{x^2} + x + 5 \le 0\).
b) \( - 3{x^2} + 2\sqrt 3 x - 1 \ge 0\).
c) \( - {x^2} + 2x + 1 > 0\).
Giải:
a) Tam thức \(f(x) = 3{x^2} + x + 5\) có \(\Delta = - 59 < 0\), hệ số a = 3 > 0 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là \(3{x^2} + x + 5 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình vô nghiệm.
b) Tam thức \(f(x) = - 3{x^2} + 2\sqrt 3 x - 1\) có \(\Delta ' = 0\), hệ số a = -3 < 0 nên f(x) có nghiệm kép \(x = \frac{{\sqrt 3 }}{3}\) và f(x) luôn âm (cùng dấu với a) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\), tức là \( - 3{x^2} + 2\sqrt 3 x - 1 < 0\) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\).
Suy ra bất phương trình có nghiệm duy nhất \(x = \frac{{\sqrt 3 }}{3}\).
c) Tam thức \(f(x) = - {x^2} + 2x + 1\) có \(\Delta ' = 2 > 0\) nên f(x) có hai nghiệm \({x_1} = 1 - \sqrt 2 \) và \({x_2} = 1 + \sqrt 2 \).
Mặt khác, a = -1 < 0, do đó ta có bảng xét dấu sau:

Tập nghiệm của bất phương trình là \(S = \left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\).
Bất phương trình bậc hai một ẩn là một trong những chủ đề quan trọng trong chương trình Toán 10, đặc biệt là trong chương trình Chân trời sáng tạo. Việc nắm vững lý thuyết và phương pháp giải quyết các bài toán liên quan là điều cần thiết để đạt kết quả tốt trong học tập.
Bất phương trình bậc hai một ẩn là bất phương trình có dạng:
Trong đó, a, b, c là các số thực và a ≠ 0. x là ẩn số.
Tập nghiệm của bất phương trình bậc hai một ẩn phụ thuộc vào dấu của hệ số a và biệt thức Δ = b2 - 4ac.
Quy tắc xét dấu tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0) giúp xác định dấu của f(x) trên các khoảng xác định bởi các nghiệm của phương trình ax2 + bx + c = 0.
| Khoảng | Dấu của (x - x1) | Dấu của (x - x2) | Dấu của f(x) |
|---|---|---|---|
| x < x1 | - | - | a |
| x1 < x < x2 | + | - | -a |
| x > x2 | + | + | a |
Để giải bất phương trình bậc hai một ẩn, ta thực hiện các bước sau:
Giải bất phương trình 2x2 - 5x + 2 > 0.
Ta có a = 2, b = -5, c = 2. Δ = (-5)2 - 4(2)(2) = 25 - 16 = 9 > 0.
Phương trình 2x2 - 5x + 2 = 0 có hai nghiệm phân biệt x1 = 2 và x2 = 1/2.
Sử dụng quy tắc xét dấu, ta có:
Vậy tập nghiệm của bất phương trình là x < 1/2 hoặc x > 2.
Để nắm vững kiến thức về giải bất phương trình bậc hai một ẩn, bạn nên luyện tập thêm nhiều bài tập khác nhau. Hãy tham khảo các bài tập trong SGK Toán 10 Chân trời sáng tạo và các tài liệu tham khảo khác.
Chúc bạn học tập tốt!