Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 45, 46, 47 sách giáo khoa Toán 10 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Quan sát đồ thị hàm số y = f(x) = {x^2} rồi so sánh f(x1) và f(x2) (với x1 < x2) trong từng trường hợp sau: a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
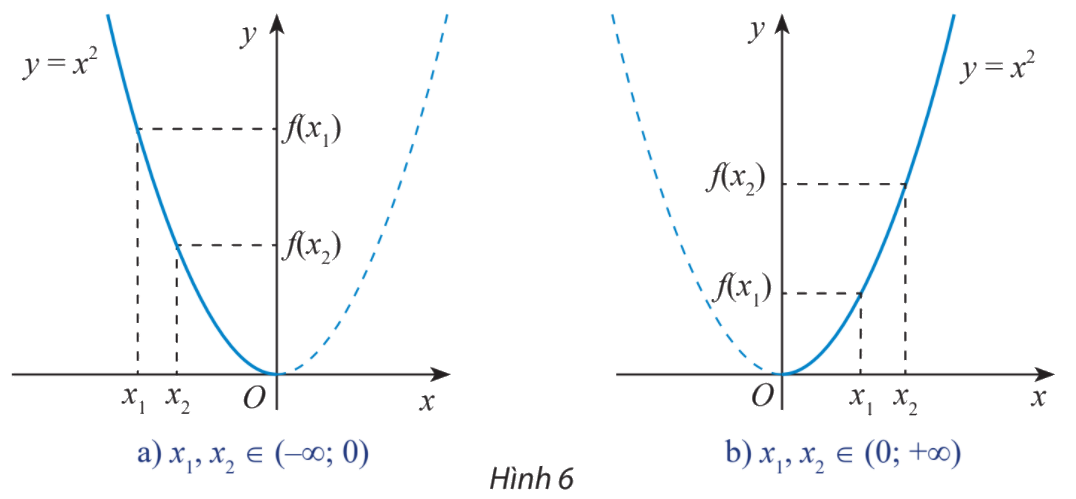
Quan sát đồ thị hàm số \(y = f(x) = {x^2}\) rồi so sánh \(f({x_1})\) và \(f({x_2})\) (với \({x_1} < {x_2}\)) trong từng trường hợp sau:
Phương pháp giải:
Trên tia Oy, giá trị nào gần gốc tọa độ hơn thì nhỏ hơn.
Lời giải chi tiết:
a) \(f({x_1}) > f({x_2})\)
b) \(f({x_1}) < f({x_2})\)
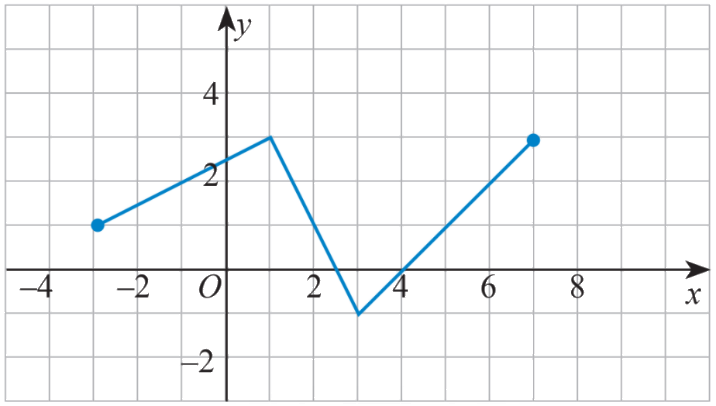
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
Phương pháp giải:
a) Quan sát đồ thị trên các khoảng (-3; 1), (1;3), (3;7)
Khi hàm số đồng biến trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải.
Khi hàm số nghịch biến trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
b)
Bước 1: Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Bước 2: So sánh \(f({x_1}) = 5{x_1}^2\) và \(f({x_2}) = 5{x_2}^2\)
Bước 3: Kết luận tính đồng biến, nghịch biến
+ Nếu \(f({x_1}) < f({x_2})\) thì hàm số đồng biến trên khoảng (2; 5)
+ Nếu \(f({x_1}) > f({x_2})\) thì hàm số nghịch biến trên khoảng (2; 5)
Lời giải chi tiết:
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
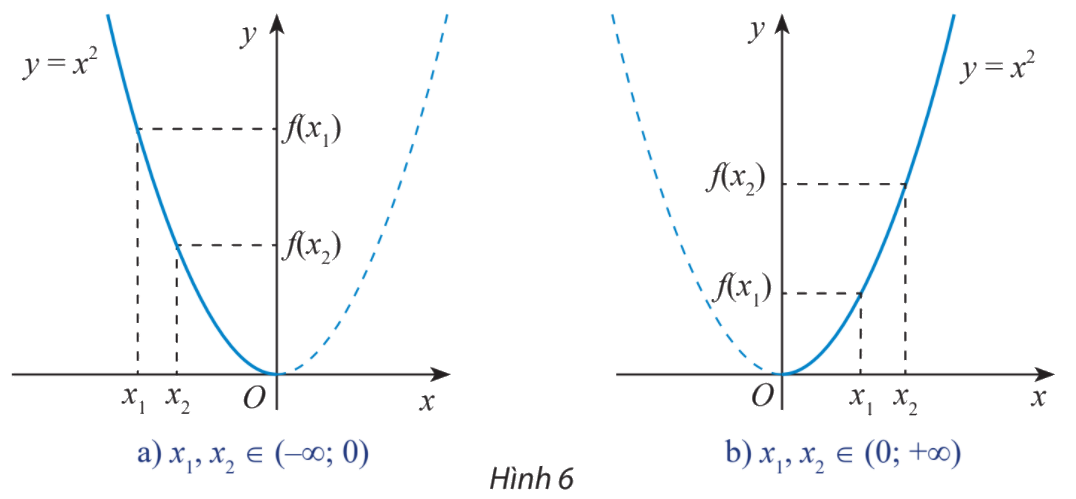
Quan sát đồ thị hàm số \(y = f(x) = {x^2}\) rồi so sánh \(f({x_1})\) và \(f({x_2})\) (với \({x_1} < {x_2}\)) trong từng trường hợp sau:
Phương pháp giải:
Trên tia Oy, giá trị nào gần gốc tọa độ hơn thì nhỏ hơn.
Lời giải chi tiết:
a) \(f({x_1}) > f({x_2})\)
b) \(f({x_1}) < f({x_2})\)
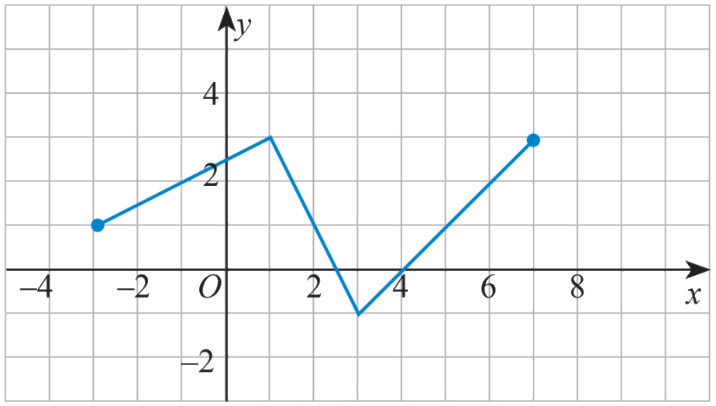
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
Phương pháp giải:
a) Quan sát đồ thị trên các khoảng (-3; 1), (1;3), (3;7)
Khi hàm số đồng biến trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải.
Khi hàm số nghịch biến trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.
b)
Bước 1: Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Bước 2: So sánh \(f({x_1}) = 5{x_1}^2\) và \(f({x_2}) = 5{x_2}^2\)
Bước 3: Kết luận tính đồng biến, nghịch biến
+ Nếu \(f({x_1}) < f({x_2})\) thì hàm số đồng biến trên khoảng (2; 5)
+ Nếu \(f({x_1}) > f({x_2})\) thì hàm số nghịch biến trên khoảng (2; 5)
Lời giải chi tiết:
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về vectơ, đặc biệt là các phép toán trên vectơ và ứng dụng của vectơ trong hình học. Các bài tập trang 45, 46, 47 yêu cầu học sinh vận dụng các định nghĩa, tính chất và công thức đã học để giải quyết các bài toán cụ thể.
Bài tập này yêu cầu học sinh xác định tọa độ của một vectơ dựa trên tọa độ của các điểm đầu và điểm cuối của vectơ. Để giải bài tập này, học sinh cần nắm vững công thức tính tọa độ của vectơ: Nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ (xB - xA, yB - yA).
Ví dụ: Cho A(1, 2) và B(3, 5). Tìm tọa độ của vectơ AB. Giải: Vectơ AB có tọa độ (3 - 1, 5 - 2) = (2, 3).
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ, nhân với một số thực của các vectơ. Để giải bài tập này, học sinh cần nắm vững các quy tắc sau:
Ví dụ: Cho vectơ a = (1, 2) và b = (3, 4). Tính vectơ a + b và 2a. Giải: a + b = (1 + 3, 2 + 4) = (4, 6). 2a = (2*1, 2*2) = (2, 4).
Bài tập này yêu cầu học sinh sử dụng vectơ để chứng minh các tính chất hình học, chẳng hạn như chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, hoặc tính diện tích của một hình.
Ví dụ: Cho ba điểm A(1, 2), B(3, 4), C(5, 6). Chứng minh rằng ba điểm A, B, C thẳng hàng. Giải: Ta tính vectơ AB = (3 - 1, 4 - 2) = (2, 2) và vectơ AC = (5 - 1, 6 - 2) = (4, 4). Ta thấy vectơ AC = 2 vectơ AB, do đó ba điểm A, B, C thẳng hàng.
Khi giải các bài tập về vectơ, học sinh cần chú ý các điểm sau:
Ngoài SGK Toán 10 tập 1 chương trình Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 45, 46, 47 SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!