Bài 7 trang 119 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Bài tập này thường gặp trong các kỳ kiểm tra và thi cử, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7 trang 119 SGK Toán 10 tập 1, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin giải các bài tập tương tự.
Kết quả bài kiểm tra giữa kì cả các bạn học sinh lớp 10A, 10B, 10C được thống kê ở các biểu đồ dưới đây.
Đề bài
Kết quả bài kiểm tra giữa kì cả các bạn học sinh lớp 10A, 10B, 10C được thống kê ở các biểu đồ dưới đây.
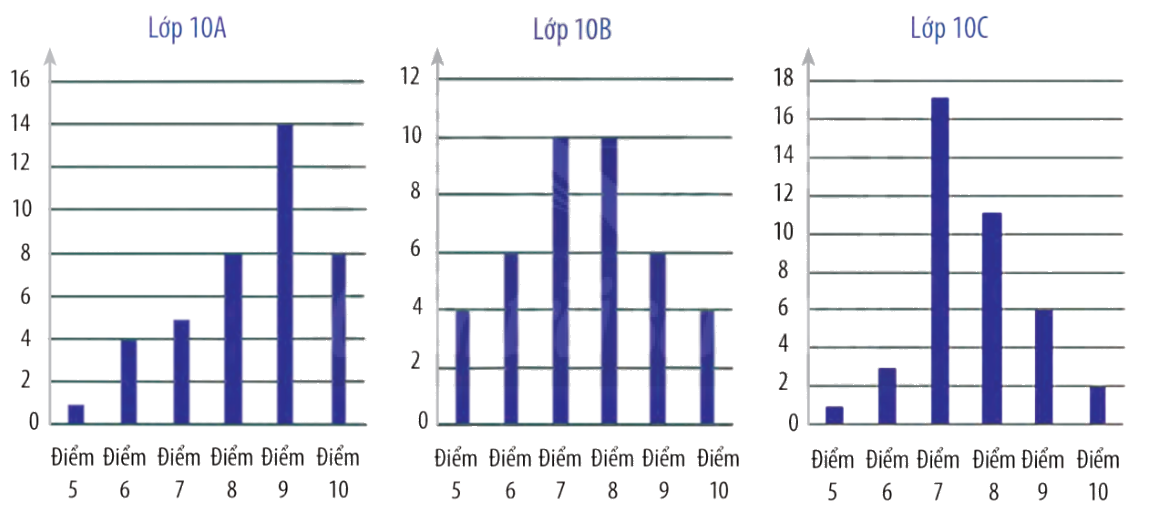
a) Hãy lập thống kê số lượng học sinh theo điểm số ở mỗi lớp.
b) Hãy so sánh điểm số của học sinh các lớp đó theo số trung bình, trung vị và mốt.
Phương pháp giải - Xem chi tiết
b)
+) Số trung bình: \(\overline x = \frac{{{x_1}.{f_1} + {x_2}.{f_2} + ... + {x_m}.{f_m}}}{{{f_1} + {f_2} + ... + {f_m}}}\)
+) Trung vị: \({M_e}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
Bước 2: Tình trung vị: \({M_e} = \left\{ \begin{array}{l}{X_{k + 1}}\quad \quad \quad \quad \quad (n = 2k + 1)\\\frac{1}{2}({X_k} + {X_{k + 1}})\quad \;\,(n = 2k)\end{array} \right.\)
+) Mốt \({M_o}\) là giá trị có tần số lớn nhất. (Một mẫu có thể có nhiều mốt)
Lời giải chi tiết
a)
Lớp 10A | Điểm | 5 | 6 | 7 | 8 | 9 | 10 |
Số HS | 1 | 4 | 5 | 8 | 14 | 8 | |
Lớp 10B | Điểm | 5 | 6 | 7 | 8 | 9 | 10 |
Số HS | 4 | 6 | 10 | 10 | 6 | 4 | |
Lớp 10C | Điểm | 5 | 6 | 7 | 8 | 9 | 10 |
Số HS | 1 | 3 | 17 | 11 | 6 | 2 |
b)
+) Lớp 10A
Số trung bình \(\overline x = \frac{{5.1 + 6.4 + 7.5 + 8.8 + 9.14 + 10.8}}{{1 + 4 + 5 + 8 + 14 + 8}} = 8,35\)
Sắp sếp số liệu theo thứ tự không giảm, ta được: \(5,6,6,6,6,7,7,7,7,7,\underbrace {8,...,8}_8,\underbrace {9,...,9}_{14},\underbrace {10,...,10}_8\)
Do \(n = 40\), là số chẵn nên trung vị là: \({M_e} = \frac{1}{2}(9 + 9) = 9\)
Mốt \({M_e} = 9\)
+) Lớp 10B
Số trung bình \(\overline x = \frac{{5.4 + 6.6 + 7.10 + 8.10 + 9.6 + 10.4}}{{4 + 6 + 10 + 10 + 6 + 4}} = 7,5\)
Sắp sếp số liệu theo thứ tự không giảm, ta được: \(5,5,5,5,\underbrace {6,..,6}_6,\underbrace {7,...,7}_{10},\underbrace {8,...,8}_{10},\underbrace {9,...,9}_6,10,10,10,10\)
Do \(n = 40\), là số chẵn nên trung vị là: \({M_e} = \frac{1}{2}(7 + 8) = 7,5\)
Mốt \({M_e} = 7;{M_e} = 8.\)
+) Lớp 10C
Số trung bình \(\overline x = \frac{{5.1 + 6.3 + 7.17 + 8.11 + 9.6 + 10.2}}{{1 + 3 + 17 + 11 + 6 + 2}} = 7,6\)
Sắp sếp số liệu theo thứ tự không giảm, ta được: \(5,6,6,6,\underbrace {7,...,7}_{17},\underbrace {8,...,8}_{11},\underbrace {9,...,9}_6,10,10\)
Do \(n = 40\), là số chẵn nên trung vị là: \({M_e} = \frac{1}{2}(7 + 7) = 7\)
Mốt \({M_e} = 7\)
+) So sánh:
Số trung bình: \(8,35 > 7,6 > 7,5\) => Điểm số của HS các lớp theo thứ tự giảm dần là 10A, 10C, 10B.
Số trung vị: \(9 > 7,5 > 7\)=> Điểm số của HS các lớp theo thứ tự giảm dần là 10A, 10B, 10C.
Mốt: Lớp 10A có 14 điểm 9, Lớp 10B có 10 điểm 7 và 10 điểm 8, Lớp 10C có 17 điểm 7. Do đó so sánh theo mốt thì điểm số các lớp giảm dàn theo thứ tự là: 10A, 10B, 10C.
Bài 7 trang 119 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng vào giải quyết các bài toán hình học. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và các tính chất liên quan.
Bài 7 yêu cầu học sinh thực hiện các thao tác với vectơ, thường là tìm vectơ tổng, hiệu, tích của một số với vectơ, hoặc chứng minh một đẳng thức vectơ nào đó. Đề bài có thể cho trước các điểm trong mặt phẳng hoặc không gian, và yêu cầu tìm vectơ biểu diễn một đoạn thẳng hoặc một hình hình học nào đó.
Giả sử đề bài yêu cầu tìm vectơ AB, biết tọa độ của điểm A là (xA, yA) và tọa độ của điểm B là (xB, yB). Khi đó, vectơ AB được tính như sau:
AB = (xB - xA, yB - yA)
Tương tự, nếu đề bài yêu cầu tìm độ dài của vectơ AB, ta sử dụng công thức:
|AB| = √((xB - xA)2 + (yB - yA)2)
Để củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán online uy tín.
Giải bài 7 trang 119 SGK Toán 10 tập 1 – Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về vectơ và áp dụng linh hoạt các phép toán vectơ. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!