Bài 10 trang 103 SGK Toán 10 tập 1 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 103 SGK Toán 10 tập 1 Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.
Đề bài
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \).
Phương pháp giải - Xem chi tiết
Bước 1: Qua M kẻ các đường thẳng song song với AB, AC, BC.
Bước 2: Xác định các tam giác đều, hình bình hành sau đó áp dụng vào biểu thức vectơ, trong tam giác đều thì đường cao vừa là trung tuyến, quy tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (với ABCD là hình bình hành).
Bước 3: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \), tính chất trọng tâm của tam giác \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) (với G là trọng tâm của tam giác ABC).
Lời giải chi tiết
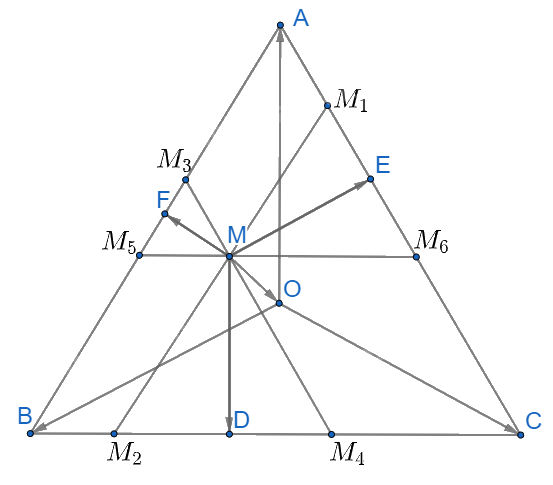
\(\overrightarrow {MD} {\rm{\;}} + \overrightarrow {ME} {\rm{\;}} + \overrightarrow {MF} {\rm{\;}} = \left( {\overrightarrow {MO} {\rm{\;}} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} {\rm{\;}} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} {\rm{\;}} + \overrightarrow {OF} } \right)\) (quy tắc ba điểm).
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\).
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = {60^\circ }\) (góc so le trong với các góc của tam giác đều).
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều.
Do đó MD, ME, MF là các đường cao, đồng thời là đường trung tuyến của các tam giác đều trên.
Áp dụng tính chất đường trung tuyến, ta có:
\(\overrightarrow {ME} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} {\rm{\;}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} {\rm{\;}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} {\rm{\;}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} {\rm{\;}} + \overrightarrow {ME} {\rm{\;}} + \overrightarrow {MF} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} {\rm{\;}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} {\rm{\;}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} {\rm{\;}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} {\rm{\;}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} {\rm{\;}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} {\rm{\;}} + \overrightarrow {M{M_6}} } \right)\) (hoán vị)
\( = \frac{1}{2}\overrightarrow {MA} {\rm{\;}} + \frac{1}{2}\overrightarrow {MB} {\rm{\;}} + \frac{1}{2}\overrightarrow {MC} {\rm{\;}}\) (quy tắc hình bình hành, dễ dàng chứng minh các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành do có các cặp cạnh đối song song).
\( = \frac{1}{2}\left( {\overrightarrow {MA} {\rm{\;}} + \overrightarrow {MB} {\rm{\;}} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} {\rm{\;}} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} {\rm{\;}} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} {\rm{\;}} + \overrightarrow {OC} } \right)} \right)\) (quy tắc ba điểm)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} {\rm{\;}} + \left( {\overrightarrow {OA} {\rm{\;}} + \overrightarrow {OB} {\rm{\;}} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{3}{2}\left( {\overrightarrow {MO} + \overrightarrow 0 } \right)\) (tính chất trọng tâm)
Vậy \(\overrightarrow {MD} {\rm{\;}} + \overrightarrow {ME} {\rm{\;}} + \overrightarrow {MF} {\rm{\;}} = \frac{3}{2}\overrightarrow {MO} \).
Bài 10 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Nội dung bài tập: Bài 10 yêu cầu học sinh sử dụng kiến thức về vectơ để giải quyết một bài toán cụ thể liên quan đến hình học. Bài toán thường yêu cầu chứng minh một đẳng thức vectơ, tìm một điểm thỏa mãn một điều kiện nào đó, hoặc tính một độ dài, diện tích.
(Ở đây sẽ là lời giải chi tiết của bài tập, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm bắt được phương pháp giải bài tập.)
Ví dụ minh họa:
Giả sử bài tập yêu cầu chứng minh rằng tứ giác ABCD là hình bình hành. Để chứng minh điều này, ta có thể sử dụng tính chất của vectơ như sau:
Nếu cả hai điều kiện trên được thỏa mãn, thì tứ giác ABCD là hình bình hành.
Để hiểu sâu hơn về vectơ và các ứng dụng của nó, các em học sinh có thể tham khảo thêm các bài tập tương tự trong SGK và sách bài tập Toán 10. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học Toán 10 online để được hướng dẫn và giải đáp thắc mắc.
Các bài tập luyện tập tương tự:
Khi giải bài tập về vectơ, các em học sinh cần lưu ý những điều sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin giải bài 10 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |