Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 52, 53 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 3 tập trung vào các kiến thức về...
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp. Tìm khoảng đồng biến, khoảng nghịch biến của hàm số y = 2x^2 - 6x + 11. Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?
Tìm khoảng đồng biến, khoảng nghịch biến của hàm số \(y = 2{x^2} - 6x + 11.\) Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?
Phương pháp giải:
Lập bảng biến thiên, xác định khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số.
Lời giải chi tiết:
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 6)}}{{2.2}} = \frac{3}{2};{y_S} = 2.{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 11 = \frac{{13}}{2}.\)
Hay \(S\left( {\frac{3}{2};\frac{{13}}{2}} \right).\)
Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:
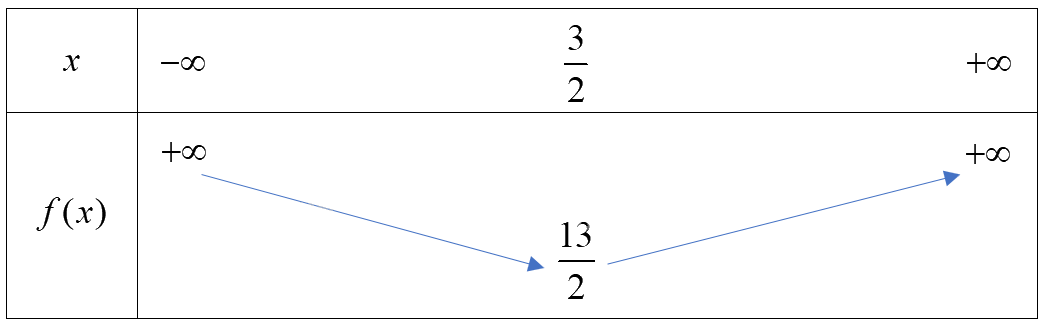
Hàm số đồng biến trên khoảng \((\frac{3}{2}; + \infty )\) và nghịch biến trên khoảng \(( - \infty ;\frac{3}{2})\)
Hàm số đạt giá trị nhỏ nhất bằng \(\frac{{13}}{2}\) khi \(x = \frac{3}{2}\)
Do đó hàm số không thể đạt giá trị bằng -1 vì \( - 1 < \frac{{13}}{2}.\)
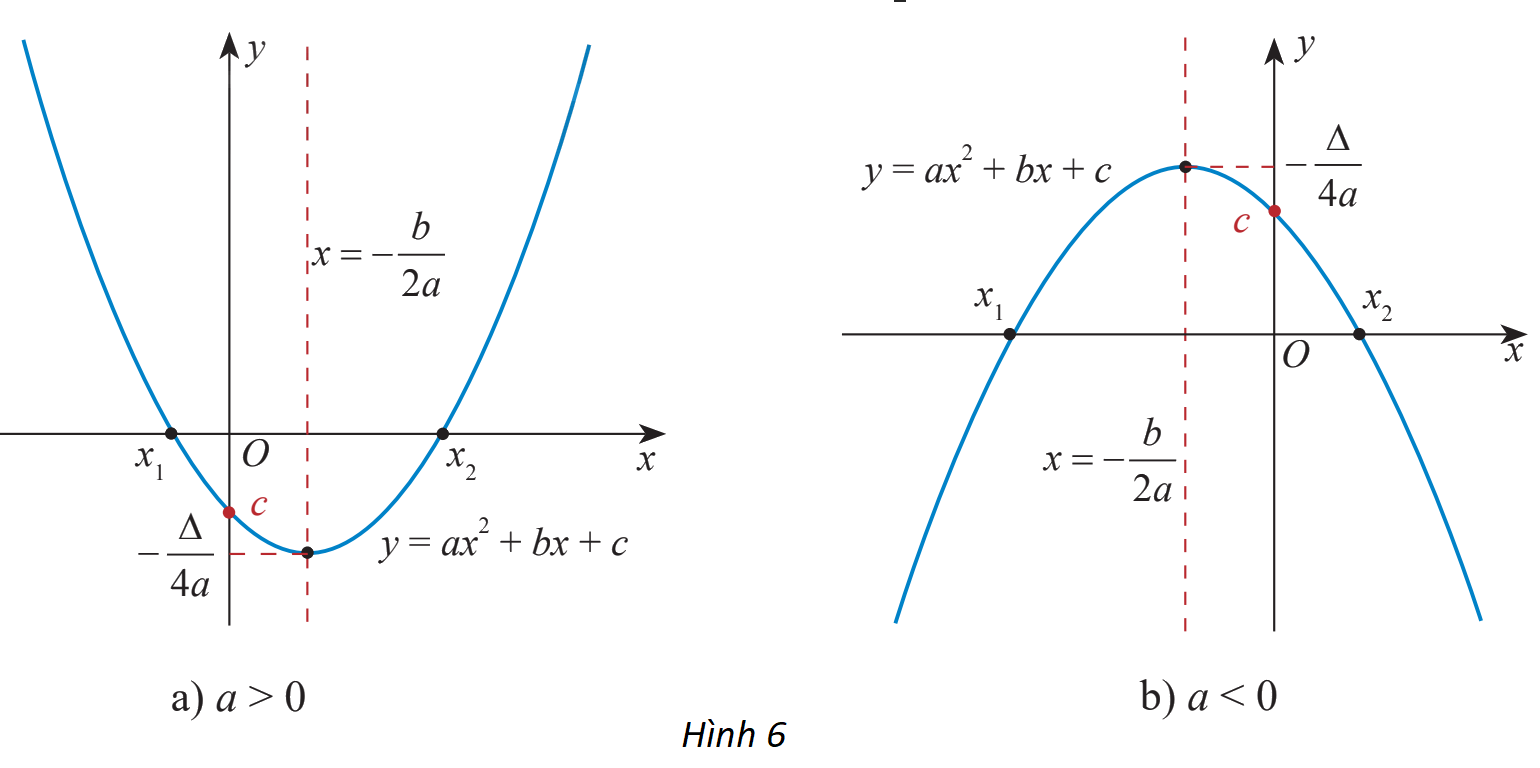
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.
Phương pháp giải:
Quan sát đồ thị hàm số trên các khoảng \(( - \infty ; - \frac{b}{{2a}})\) và \(( - \frac{b}{{2a}}; + \infty )\)
Trên (a’; b’): đồ thị có dạng đi lên từ trái sang phải thì hàm số đó đồng biến trên (a’;b’).
Trên (c; d): đồ thị có dạng đi xuống từ trái sang phải thì hàm số đó nghịch biến trên (c;d).
Lời giải chi tiết:
a)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)
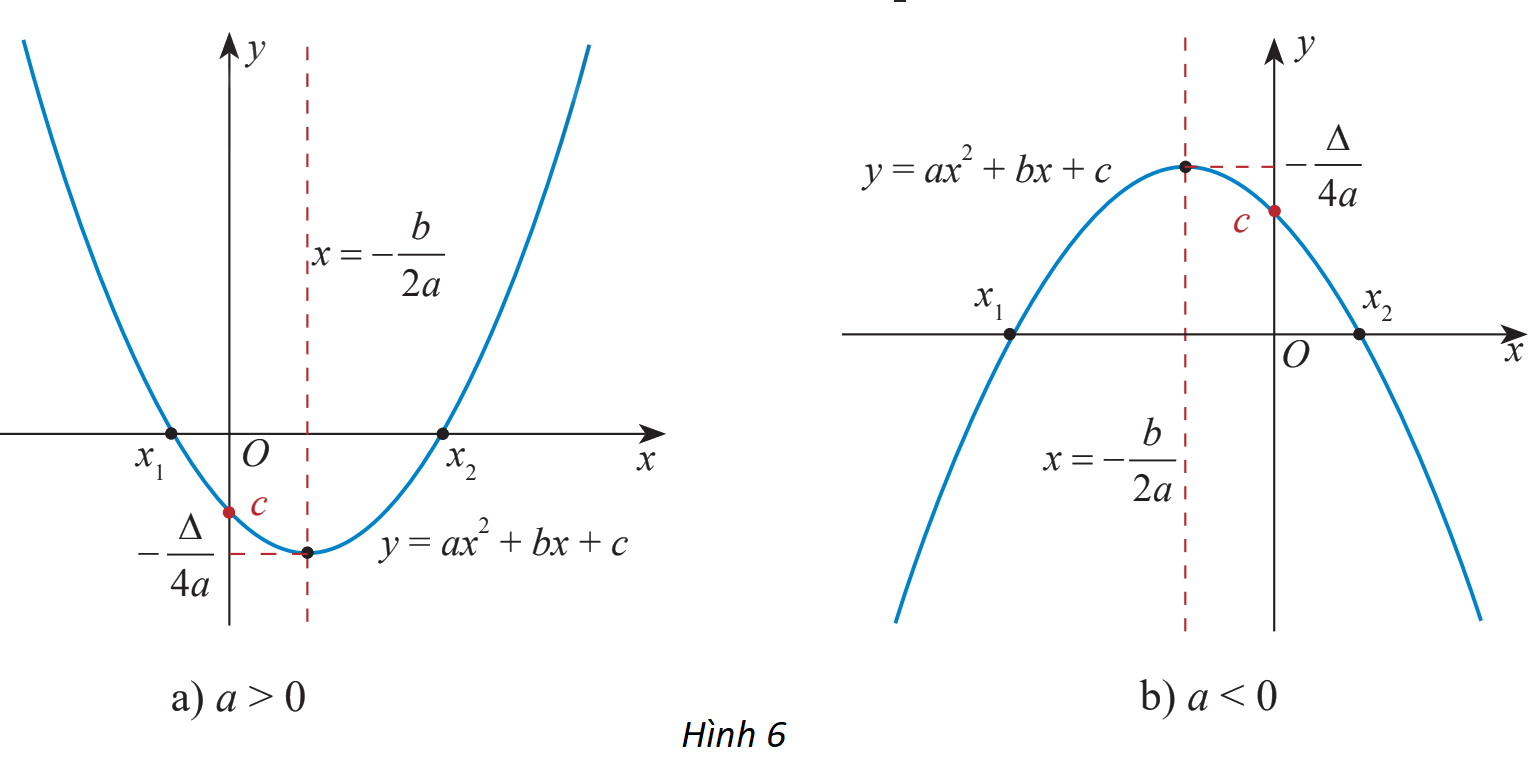
Từ đồ thị hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.
Phương pháp giải:
Quan sát đồ thị hàm số trên các khoảng \(( - \infty ; - \frac{b}{{2a}})\) và \(( - \frac{b}{{2a}}; + \infty )\)
Trên (a’; b’): đồ thị có dạng đi lên từ trái sang phải thì hàm số đó đồng biến trên (a’;b’).
Trên (c; d): đồ thị có dạng đi xuống từ trái sang phải thì hàm số đó nghịch biến trên (c;d).
Lời giải chi tiết:
a)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \frac{b}{{2a}}; + \infty )\), khoảng nghịch biến là \(( - \infty ; - \frac{b}{{2a}})\)
b)
Trên \(( - \infty ; - \frac{b}{{2a}})\) đồ thị có dạng đi lên từ trái sang phải nên hàm số đó đồng biến trên \(( - \infty ; - \frac{b}{{2a}})\)
Trên \(( - \frac{b}{{2a}}; + \infty )\) đồ thị có dạng đi xuống từ trái sang phải nên hàm số đó nghịch biến trên \(( - \frac{b}{{2a}}; + \infty )\)
Vậy hàm số có khoảng đồng biến là \(( - \infty ; - \frac{b}{{2a}})\), khoảng nghịch biến là \(( - \frac{b}{{2a}}; + \infty )\)
Tìm khoảng đồng biến, khoảng nghịch biến của hàm số \(y = 2{x^2} - 6x + 11.\) Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?
Phương pháp giải:
Lập bảng biến thiên, xác định khoảng đồng biến, nghịch biến và giá trị nhỏ nhất của hàm số.
Lời giải chi tiết:
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 6)}}{{2.2}} = \frac{3}{2};{y_S} = 2.{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 11 = \frac{{13}}{2}.\)
Hay \(S\left( {\frac{3}{2};\frac{{13}}{2}} \right).\)
Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:
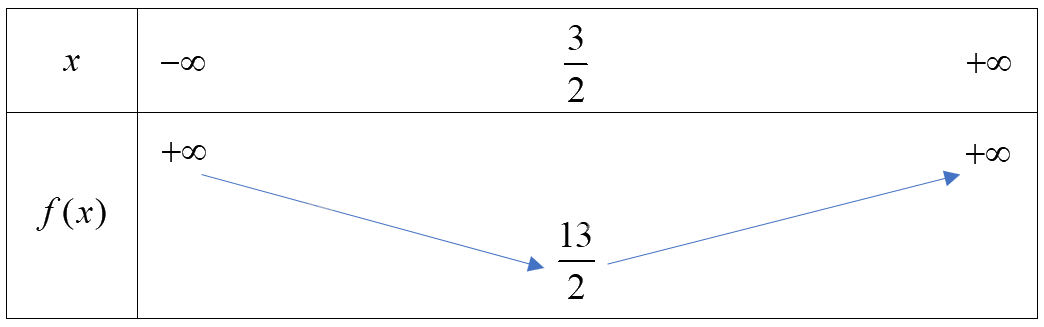
Hàm số đồng biến trên khoảng \((\frac{3}{2}; + \infty )\) và nghịch biến trên khoảng \(( - \infty ;\frac{3}{2})\)
Hàm số đạt giá trị nhỏ nhất bằng \(\frac{{13}}{2}\) khi \(x = \frac{3}{2}\)
Do đó hàm số không thể đạt giá trị bằng -1 vì \( - 1 < \frac{{13}}{2}.\)
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo thường xoay quanh các khái niệm và ứng dụng của... (nội dung cụ thể của mục 3). Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập trong mục này là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các chương tiếp theo.
Đề bài: ...
Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Đề bài: ...
Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Đề bài: ...
Lời giải: ... (Giải chi tiết từng bước, kèm theo giải thích rõ ràng)
Để giải các bài tập trong mục 3 một cách hiệu quả, các em cần nắm vững các phương pháp sau:
Ngoài các bài tập trong SGK, các em có thể tìm hiểu thêm các bài tập tương tự trên các trang web học toán online hoặc trong các sách tham khảo. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Trong quá trình giải bài tập, các em nên chú ý đến các đơn vị đo lường, các dấu hiệu đặc biệt và các trường hợp ngoại lệ. Việc cẩn thận và tỉ mỉ sẽ giúp các em tránh được những sai sót không đáng có.
Kiến thức về... (nội dung mục 3) có ứng dụng rộng rãi trong thực tế, ví dụ như...
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày ở trên, các em học sinh sẽ hiểu rõ hơn về mục 3 trang 52, 53 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Độ khó | Lời giải |
|---|---|---|
| Bài 1 | Dễ | Đã giải ở trên |
| Bài 2 | Trung bình | Đã giải ở trên |
| Bài 3 | Khó | Đã giải ở trên |