Bài 6 trang 59 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp và các tính chất của chúng để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 59 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước).
Đề bài
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người muốn thực hiện một cú nhày bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.
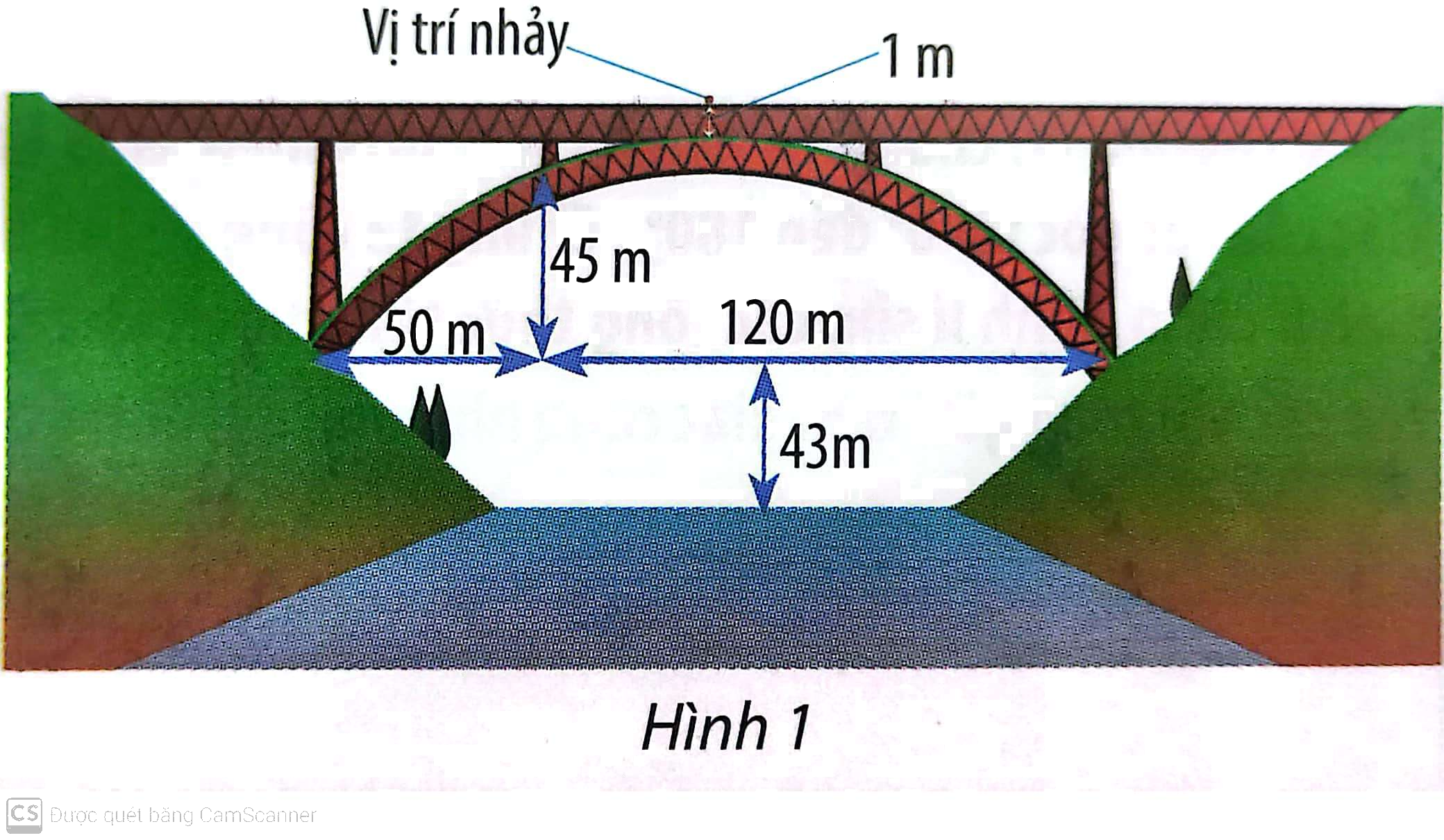
Phương pháp giải - Xem chi tiết
Gắn hệ trục tọa độ, gọi công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
Xác định hàm số và xác định tung độ của đỉnh.
Lời giải chi tiết
Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
Chọn hệ trục tọa độ Oxy như hình dưới:
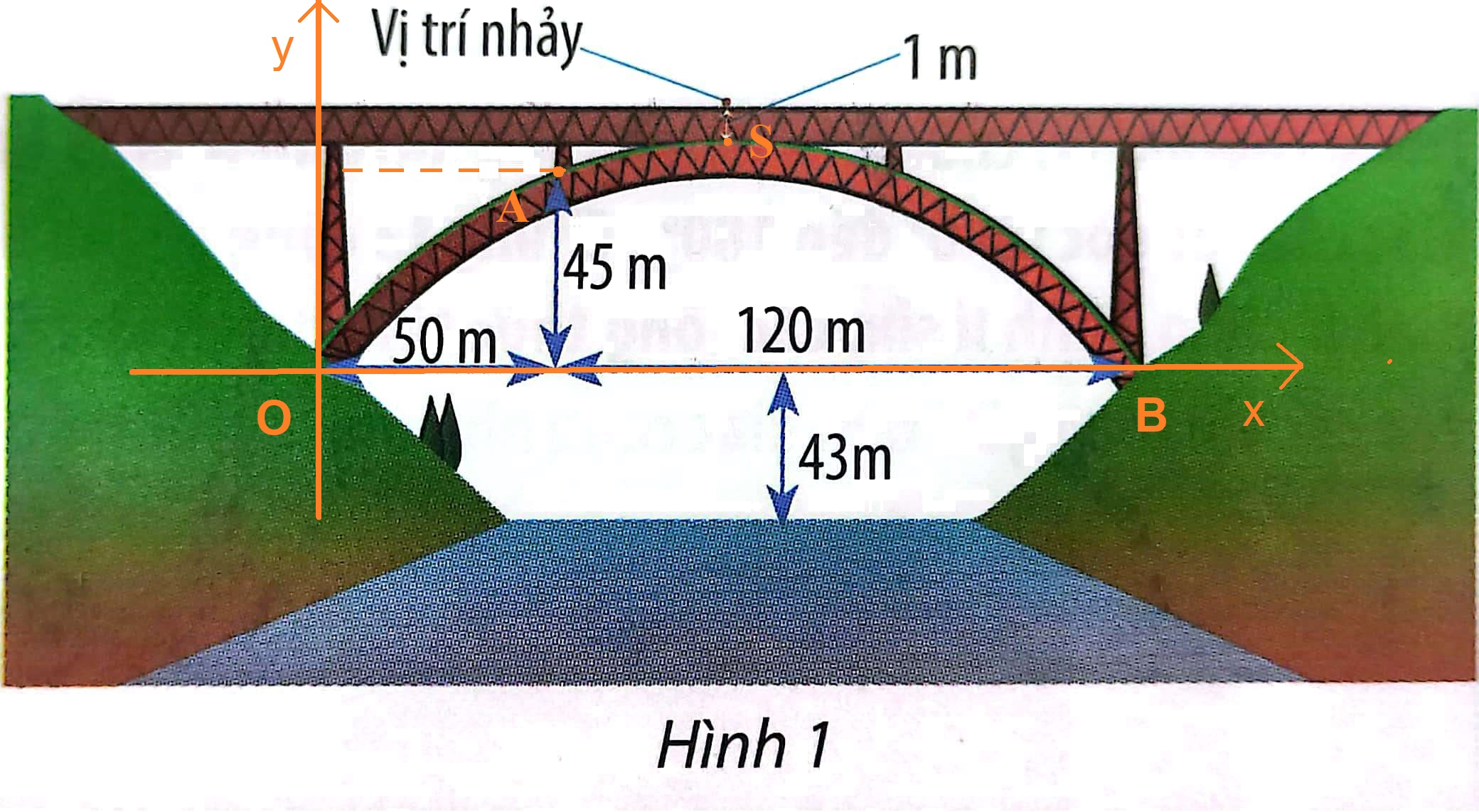
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)
\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)
\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)
Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)
Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)
Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)
Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)
Bài 6 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về tập hợp và các phép toán trên tập hợp. Bài tập này thường yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán hợp, giao, hiệu, bù, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 6 thường bao gồm các câu hỏi nhỏ, mỗi câu hỏi yêu cầu học sinh thực hiện một thao tác cụ thể với tập hợp. Ví dụ:
Để giải bài tập 6 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo hiệu quả, học sinh cần nắm vững các kiến thức sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng câu hỏi. (Ở đây sẽ là lời giải chi tiết cho từng phần của bài 6, ví dụ:)
Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Tìm A ∪ B.
Lời giải: A ∪ B = {1, 2, 3, 4, 5, 6, 7}
Cho A = {1, 2, 3} và B = {2, 4, 6}. Tìm A ∩ B.
Lời giải: A ∩ B = {2}
Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A \ B.
Lời giải: A \ B = {1, 2}
Ví dụ 1: Cho A = {a, b, c} và B = {b, c, d}. Tìm A ∪ B và A ∩ B.
Lời giải:
Để củng cố kiến thức về tập hợp và các phép toán trên tập hợp, các em học sinh có thể tự giải các bài tập sau:
Bài 6 trang 59 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh nắm vững kiến thức về tập hợp và các phép toán trên tập hợp. Bằng cách nắm vững các kiến thức và phương pháp giải bài tập, các em học sinh có thể tự tin giải quyết các bài toán liên quan đến tập hợp.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các ví dụ minh họa trên sẽ giúp các em học sinh hiểu rõ hơn về bài tập này và đạt kết quả tốt trong môn Toán 10.