Bài 1 trang 93 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi hiểu rằng việc giải các bài tập Toán 10 có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 1 trang 93 SGK Toán 10 tập 1 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
Đề bài
Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
a) \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0;} \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
Phương pháp giải - Xem chi tiết
a) Thay vectơ \(\overrightarrow {DC} = \overrightarrow {AB} \)
b) Bước 1: chèn điểm O: \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \)
Bước 2: Sử dụng tính chất trung điểm: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \) (với M là trung điểm của đoạn thẳng AB)
Lời giải chi tiết
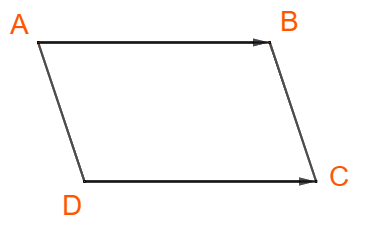
a) ABCD là hình bình hành nên \(\overrightarrow {DC} = \overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0 \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)\)
\(= \left( {\overrightarrow {MB} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BA} + \overrightarrow {DC}} \right)\)
\(= \overrightarrow {MB} + \overrightarrow {MD} \) (Vì \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} \))
Bài 1 trang 93 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng vào giải quyết các bài toán hình học. Để giúp các em học sinh hiểu rõ hơn về bài tập này, giaitoan.edu.vn xin trình bày lời giải chi tiết như sau:
Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ \overrightarrow{AM} theo hai vectơ \overrightarrow{AB} và \overrightarrow{AC}.
Ta có: \overrightarrow{AM} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})
Giải thích:
\overrightarrow{AM} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})
Bài tập này yêu cầu học sinh nắm vững các quy tắc cộng, trừ vectơ và hiểu rõ khái niệm trung điểm của một đoạn thẳng. Việc áp dụng đúng các quy tắc này sẽ giúp học sinh giải quyết bài tập một cách nhanh chóng và chính xác.
Để hiểu sâu hơn về vectơ và ứng dụng của nó trong hình học, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Chân trời sáng tạo. Ngoài ra, các em cũng có thể tìm kiếm các tài liệu học tập trực tuyến hoặc tham gia các khóa học Toán 10 online để được hướng dẫn chi tiết hơn.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập. Chúng tôi hy vọng rằng lời giải bài 1 trang 93 SGK Toán 10 tập 1 – Chân trời sáng tạo này sẽ giúp các em học tập tốt hơn và đạt kết quả cao trong môn Toán.
Chúng tôi sẽ tiếp tục cập nhật lời giải các bài tập Toán 10 tập 1 – Chân trời sáng tạo trong thời gian tới. Hãy truy cập giaitoan.edu.vn để được hỗ trợ tốt nhất!
Lưu ý:
Chúc các em học tập tốt!