Bài 4 trang 97 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Bài tập này thường gặp trong các kỳ kiểm tra và thi cử, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 97 SGK Toán 10 tập 1, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng
Đề bài
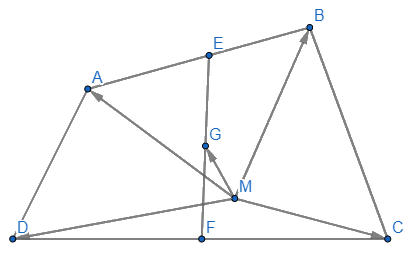
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG} \)
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc ba điểm \(\overrightarrow {MA} = \overrightarrow {MO} + \overrightarrow {OA} \) và tính chất trung điểm \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \)
(với O là trung điểm của AB)
Lời giải chi tiết
\(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EB} } \right)\\ + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FC} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FD} } \right)\end{array}\)
\( = \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} \overrightarrow { + MG} } \right) + 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) \\+ \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {FC} + \overrightarrow {FD} } \right)\)
\( = 4\overrightarrow {MG} + 2.\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MG} \) (đpcm)
Bài 4 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và mối liên hệ giữa vectơ và các yếu tố hình học.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài 4 trang 97 SGK Toán 10 tập 1 sẽ yêu cầu học sinh chứng minh một đẳng thức vectơ, tìm một điểm thỏa mãn một điều kiện nào đó hoặc tính độ dài của một đoạn thẳng.
(Nội dung lời giải chi tiết bài 4 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo sẽ được trình bày tại đây. Bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình vẽ nếu cần thiết. Ví dụ:)
Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Vì M là trung điểm của BC nên BM = MC. Do đó, BC = 2BM.
Ta có: AB + AC = AB + BC = AB + 2BM.
Mặt khác, AM = AB + BM. Suy ra 2AM = 2(AB + BM) = 2AB + 2BM.
Vậy, AB + AC = 2AM (đpcm).
Để củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 4 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.