Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 16 và 17 sách giáo khoa Toán 10 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
Lời giải cho phương trình \(\sqrt { - {x^2} + x + 1} = x\) như sau đúng hai sai?
\(\)\(\sqrt { - {x^2} + x + 1} = x\)
\( \Rightarrow - {x^2} + x + 1 = {x^2}\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow - 2{x^2} + x + 1 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 1\) hoặc \(x = - \frac{1}{2}\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 1 và \( - \frac{1}{2}\)
Phương pháp giải:
Thay nghiệm tìm được vào phương trình ban đầu ta có:
+) Thay \(x = 1\) vào phương trình \(\sqrt { - {x^2} + x + 1} = x\) ta thấy thảo mãn phương trình
+) Thay \(x = - \frac{1}{2}\) vào \(\sqrt { - {x^2} + x + 1} = x\) ta thấy không thỏa mãn phương trình
Vậy nghiệm của phương trình là \(x = 1\), suy ra lời giải như trên là sai.
Giải phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\)
Phương pháp giải:
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại và kết luận
Lời giải chi tiết:
Bình phương hai vế của phương trình đã cho, ta được:
\(3{x^2} + 27x - 41 = {\left( {2x + 3} \right)^2}\)
\( \Rightarrow 3{x^2} + 27x - 41 = 4{x^2} + 12x + 9\)
\( \Rightarrow {x^2} - 15x + 50 = 0\)
\( \Rightarrow x = 5\) và \(x = 10\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là \(x = 5\) và \(x = 10\)
Lời giải cho phương trình \(\sqrt { - {x^2} + x + 1} = x\) như sau đúng hai sai?
\(\)\(\sqrt { - {x^2} + x + 1} = x\)
\( \Rightarrow - {x^2} + x + 1 = {x^2}\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow - 2{x^2} + x + 1 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 1\) hoặc \(x = - \frac{1}{2}\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 1 và \( - \frac{1}{2}\)
Phương pháp giải:
Thay nghiệm tìm được vào phương trình ban đầu ta có:
+) Thay \(x = 1\) vào phương trình \(\sqrt { - {x^2} + x + 1} = x\) ta thấy thảo mãn phương trình
+) Thay \(x = - \frac{1}{2}\) vào \(\sqrt { - {x^2} + x + 1} = x\) ta thấy không thỏa mãn phương trình
Vậy nghiệm của phương trình là \(x = 1\), suy ra lời giải như trên là sai.
Giải phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\)
Phương pháp giải:
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại và kết luận
Lời giải chi tiết:
Bình phương hai vế của phương trình đã cho, ta được:
\(3{x^2} + 27x - 41 = {\left( {2x + 3} \right)^2}\)
\( \Rightarrow 3{x^2} + 27x - 41 = 4{x^2} + 12x + 9\)
\( \Rightarrow {x^2} - 15x + 50 = 0\)
\( \Rightarrow x = 5\) và \(x = 10\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy nghiệm của phương trình đã cho là \(x = 5\) và \(x = 10\)
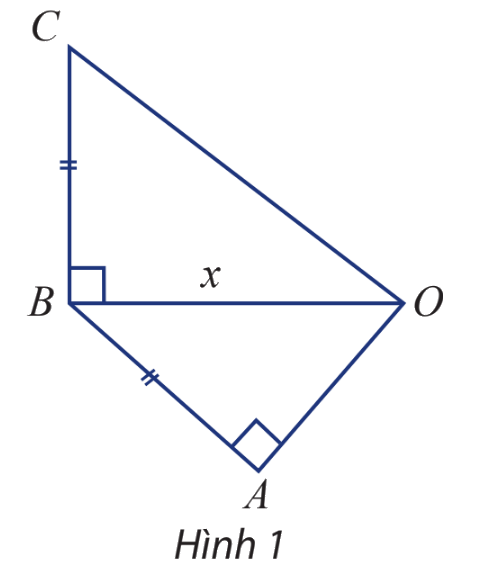
Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
a) \(OC = 3OA;\)
b) \(OC = \frac{5}{4}OB\)
Phương pháp giải:
Bước 1: Sử dụng giả thiết và áp dụng định lý pitago để biểu diễn độ dài OC và OA qua OB
Bước 2: Lập phương trình theo giả thiết \(OC = 3OA;\)\(OC = \frac{5}{4}OB\)
Bước 3: Giải phương trình
Lời giải chi tiết:
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)
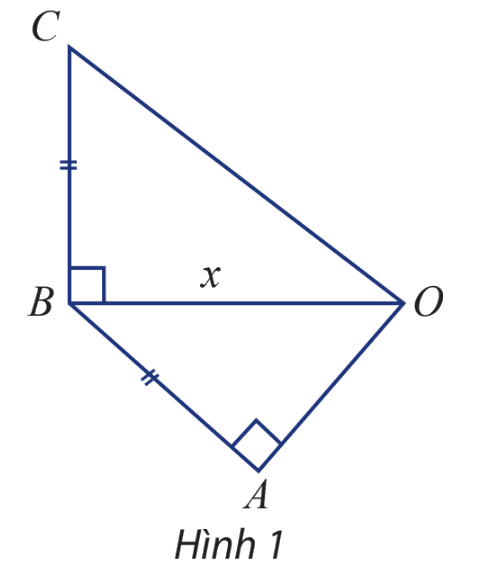
Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:
a) \(OC = 3OA;\)
b) \(OC = \frac{5}{4}OB\)
Phương pháp giải:
Bước 1: Sử dụng giả thiết và áp dụng định lý pitago để biểu diễn độ dài OC và OA qua OB
Bước 2: Lập phương trình theo giả thiết \(OC = 3OA;\)\(OC = \frac{5}{4}OB\)
Bước 3: Giải phương trình
Lời giải chi tiết:
Gọi độ dài cạnh OB là x cm \(\left( {x > 0} \right)\)
Theo giả thiết ta có \(AB = BC = OB - 1 = x - 1\)
Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:
\(OC = \sqrt {O{B^2} + B{C^2}} = \sqrt {{x^2} + {{\left( {x - 1} \right)}^2}} = \sqrt {2{x^2} - 2x + 1} \)
\(OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{x^2} - {{\left( {x - 1} \right)}^2}} = \sqrt {2x - 1} \)
a) \(OC = 3OA \Rightarrow \sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = 9\left( {2x - 1} \right)\\ \Rightarrow 2{x^2} - 20x + 10 = 0\end{array}\)
\( \Rightarrow \)\(x = 5 - 2\sqrt 5 \) và \(x = 5 + 2\sqrt 5 \)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = 3\sqrt {2x - 1} \) ta thấy cả hai đều thỏa mãn phương trình
Vậy khi \(OB = 5 - 2\sqrt 5 \) hoặc \(OB = 5 + 2\sqrt 5 \)thì \(OC = 3OA\)
b) \(OC = \frac{5}{4}OB \Rightarrow \sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\)
\(\begin{array}{l} \Rightarrow 2{x^2} - 2x + 1 = \frac{{25}}{{16}}{x^2}\\ \Rightarrow \frac{7}{{16}}{x^2} - 2x + 1 = 0\end{array}\)\(\)
\( \Rightarrow x = \frac{4}{7}\) hoặc \(x = 4\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} - 2x + 1} = \frac{5}{4}x\) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(OB = \frac{4}{7}\) hoặc \(OB = 4\) (cm) thì \(OC = \frac{5}{4}OB\)
Mục 2 của SGK Toán 10 tập 2 Chân trời sáng tạo tập trung vào việc nghiên cứu về vectơ và các phép toán vectơ cơ bản. Đây là một phần quan trọng trong chương trình học, đặt nền móng cho các kiến thức hình học nâng cao hơn. Việc nắm vững các khái niệm và kỹ năng trong mục này sẽ giúp học sinh giải quyết các bài toán liên quan đến vectơ một cách hiệu quả.
Để tìm vectơ chỉ phương của đường thẳng d, ta cần xác định hai điểm thuộc đường thẳng d. Sau đó, ta lấy hiệu tọa độ của hai điểm này để được một vectơ chỉ phương của d. Ví dụ, nếu d đi qua hai điểm A(x1, y1) và B(x2, y2), thì vectơ AB = (x2 - x1, y2 - y1) là một vectơ chỉ phương của d.
Để xác định vị trí tương đối của hai đường thẳng d1 và d2, ta xét các vectơ chỉ phương của chúng. Nếu hai vectơ chỉ phương cùng phương thì hai đường thẳng song song hoặc trùng nhau. Nếu hai vectơ chỉ phương không cùng phương thì hai đường thẳng cắt nhau.
Để tìm tọa độ của điểm M thỏa mãn điều kiện cho trước, ta thường sử dụng các công thức liên quan đến vectơ, chẳng hạn như công thức trung điểm, công thức trọng tâm, hoặc công thức biểu diễn một vectơ qua các vectơ khác.
Để chứng minh đẳng thức vectơ, ta thường sử dụng các phép toán vectơ (cộng, trừ, nhân với một số thực) để biến đổi một vế của đẳng thức về dạng tương đương với vế còn lại.
Ngoài SGK Toán 10 tập 2 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về vectơ:
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến vectơ trong SGK Toán 10 tập 2 Chân trời sáng tạo. Chúc các em học tốt!