Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn vượt qua những thách thức này.
Vẽ đồ thị hàm số f(x) = |x|
Đề bài
Vẽ đồ thị hàm số \(f\left( x \right) = \left| x \right|\) biết rằng hàm số này còn được viết như sau:
\(f(x) = \left\{ \begin{array}{l}x\quad \quad (x \ge 0)\\ - x\quad \;\;(x < 0)\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Vẽ đồ thị từng hàm trên mỗi khoảng cho trước
Lời giải chi tiết
Hàm số \(f\left( x \right) = \left| x \right|\) xác định trên \(D = \mathbb{R}\)
Trên khoảng \(( - \infty ;0)\) ta vẽ đồ thị hàm số \(y = - x\), đi qua 2 điểm \(A( - 1;1),B( - 2;2)\)
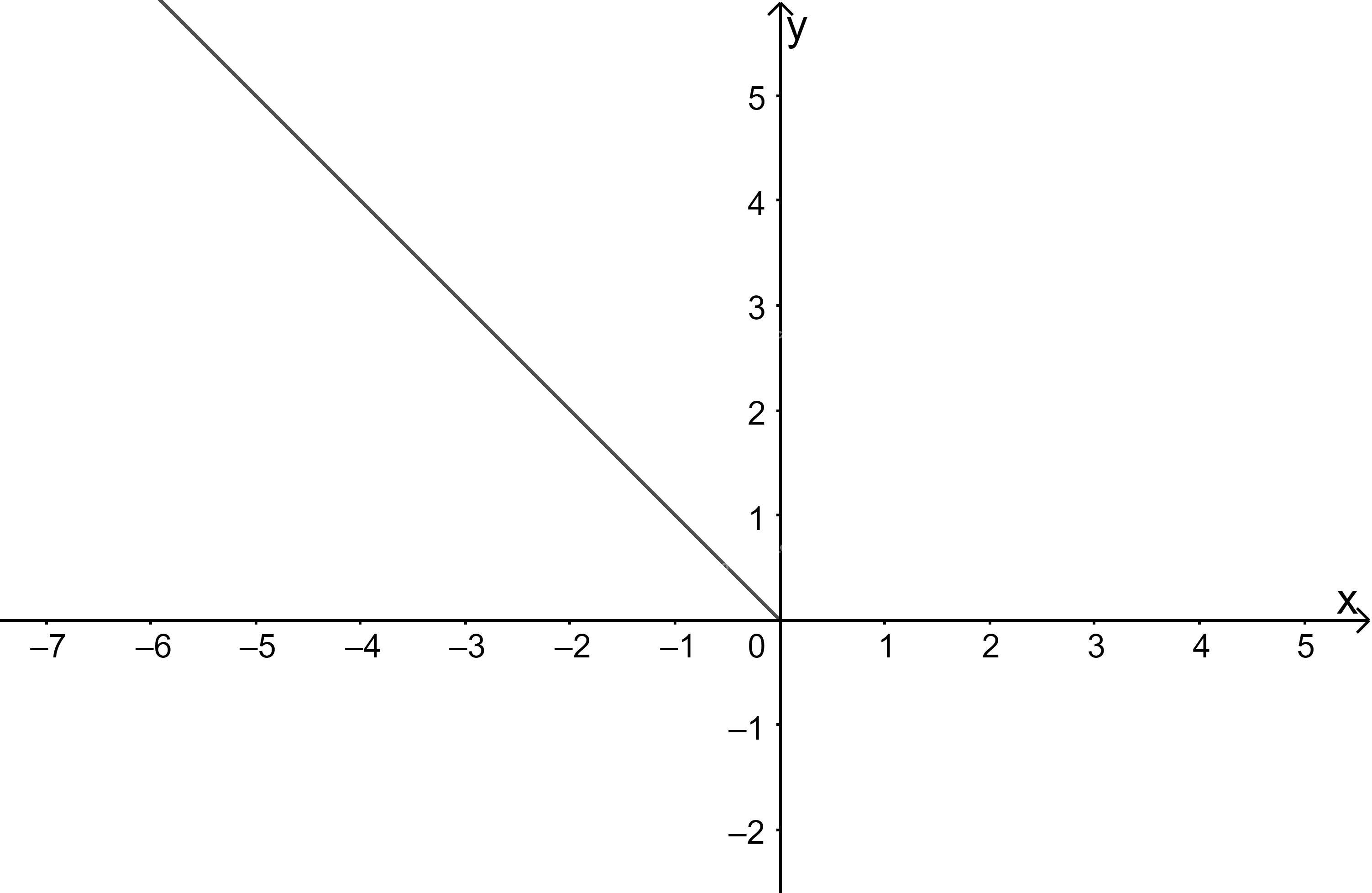
Trên khoảng \((0; + \infty )\) ta vẽ đồ thị hàm số \(y = x\), đi qua 2 điểm \(A'(1;1),B'(2;2)\)
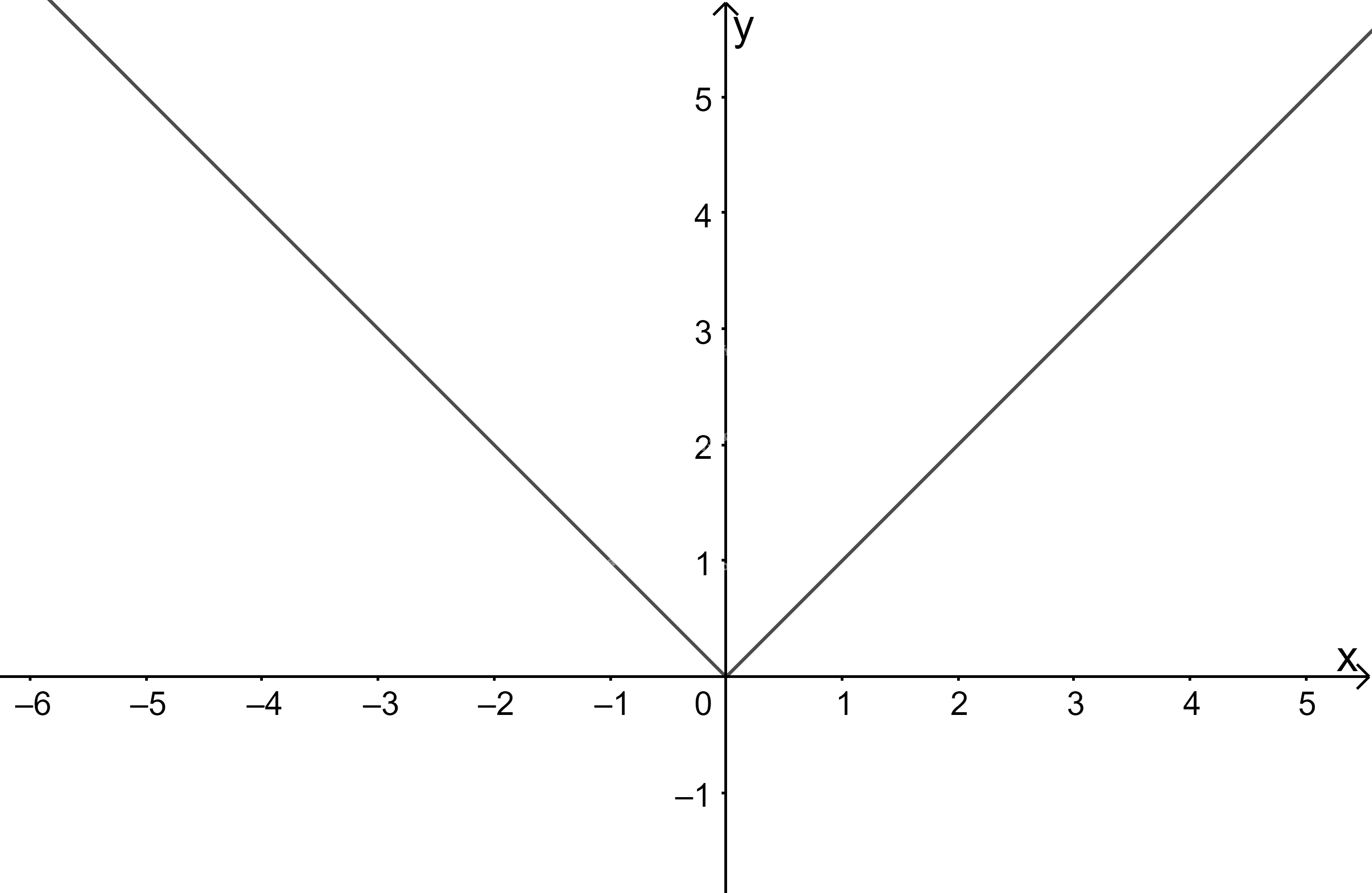
Như vậy ta được đồ thị hàm số \(f\left( x \right) = \left| x \right|\).
Bài 4 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về tập hợp, các phép toán trên tập hợp, và các tính chất cơ bản của tập hợp để giải quyết các bài toán cụ thể. Bài tập này thường yêu cầu học sinh xác định các tập hợp, tìm phần tử thuộc tập hợp, thực hiện các phép hợp, giao, hiệu của các tập hợp, và chứng minh các đẳng thức liên quan đến tập hợp.
Bài 4 trang 47 thường bao gồm các câu hỏi và bài tập sau:
Để giải bài 4 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Hãy tìm A ∪ B và A ∩ B.
Giải:
Khi giải bài tập về tập hợp, bạn cần chú ý các điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập về tập hợp, bạn có thể thực hành thêm các bài tập sau:
Bài 4 trang 47 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp bạn nắm vững kiến thức về tập hợp và các phép toán trên tập hợp. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, bạn có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!