Hàm số và đồ thị là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 10 CTST. Việc nắm vững kiến thức về hàm số không chỉ giúp học sinh giải quyết các bài toán cụ thể mà còn là nền tảng vững chắc cho các kiến thức nâng cao ở các lớp trên.
Tại giaitoan.edu.vn, chúng tôi cung cấp hệ thống lý thuyết Hàm số và đồ thị đầy đủ, chi tiết, dễ hiểu, giúp bạn tự tin chinh phục môn Toán.
1. Hàm số. Tập xác định và tập giá trị của hàm số 2. Đồ thị hàm số 3. Hàm số đồng biến, hàm số nghịch biến
1. Hàm số. Tập xác định và tập giá trị của hàm số
+) Định nghĩa:
Giả sử x và y là hai đại lượng biến thiên, \(x \in D\)
Nếu với mỗi \(x \in D\), ta xác định được y duy nhất (\(y \in \mathbb{R}\)) thì ta có một hàm số.
+) Tên gọi:
x là biến số, y là hàm số của x
D là tập xác định
\(T = \left\{ {y|x \in D} \right\}\) là tập giá trị của hàm số.
+) Ta thường kí hiệu \(f(x)\) là giá trị y tương ứng với x, nên hàm số thường viết là \(y = f(x)\)
* Chú ý
a. Hàm số cho bởi công thức mà không chỉ rõ tập xác định thì
TXĐ của hàm số \(y = f(x)\) là tập hợp tất cả các \(x \in \mathbb{R}\) sao cho \(f(x)\) có nghĩa.
b. Một hàm số có thể được cho bởi hay nhiều công thức.
2. Đồ thị hàm số
+) Hàm số \(y = f(x)\) xác định trên D, Khi đó đồ thị \((C) = \left\{ {M(x;f(x))|x \in D} \right\}\)
+) Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\)
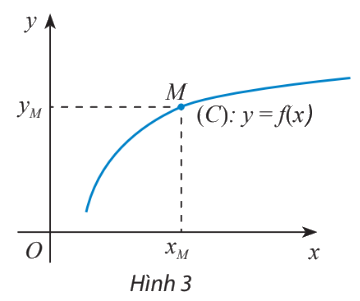
3. Hàm số đồng biến, hàm số nghịch biến
+) Định nghĩa: Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\)
- Hàm số đồng biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
- Hàm số nghịch biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
+) Quan sát đồ thị: trên khoảng \((a;b)\)
- Hàm số đồng biến (tăng) thì đồ thị có dạng đi lên từ trái sang phải.
- Hàm số nghịch biến (giảm) thì đồ thị có dạng đi xuồng từ trái sang phải.
Chương trình Toán 10 CTST, Hàm số và đồ thị đóng vai trò then chốt trong việc xây dựng nền tảng toán học vững chắc. Nắm vững lý thuyết và kỹ năng vẽ đồ thị hàm số là điều kiện cần thiết để giải quyết các bài toán liên quan và tiếp thu kiến thức ở các lớp trên.
Hàm số là một quy tắc tương ứng giữa mỗi phần tử của tập hợp A (tập xác định) với duy nhất một phần tử của tập hợp B (tập giá trị). Ký hiệu: y = f(x), trong đó x thuộc A, y thuộc B.
Trong chương trình Toán 10 CTST, học sinh sẽ được làm quen với một số loại hàm số cơ bản sau:
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm có tọa độ (x; f(x)) với mọi x thuộc tập xác định của hàm số.
Cách vẽ đồ thị hàm số:
Các tính chất quan trọng của hàm số bao gồm:
Ví dụ 1: Xét hàm số y = 2x + 1. Đây là hàm số bậc nhất với a = 2 > 0, do đó hàm số đồng biến trên R. Đồ thị của hàm số là một đường thẳng cắt trục Oy tại điểm (0; 1) và có hệ số góc là 2.
Ví dụ 2: Xét hàm số y = x2. Đây là hàm số bậc hai với a = 1 > 0, do đó hàm số nghịch biến trên khoảng (-∞; 0) và đồng biến trên khoảng (0; +∞). Đồ thị của hàm số là một parabol có đỉnh tại gốc tọa độ và mở lên trên.
Để củng cố kiến thức về Lý thuyết Hàm số và đồ thị, bạn có thể thực hành giải các bài tập sau:
Hy vọng với những kiến thức và ví dụ minh họa trên, bạn đã có cái nhìn tổng quan và hiểu rõ hơn về Lý thuyết Hàm số và đồ thị - SGK Toán 10 CTST. Chúc bạn học tập tốt!