Chào mừng bạn đến với bài học về lý thuyết các phép toán trên tập hợp trong chương trình Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các phép toán trên tập hợp, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu về hợp, giao, hiệu và phần bù của các tập hợp, cùng với các tính chất và ứng dụng thực tế của chúng. Hãy bắt đầu ngay thôi!
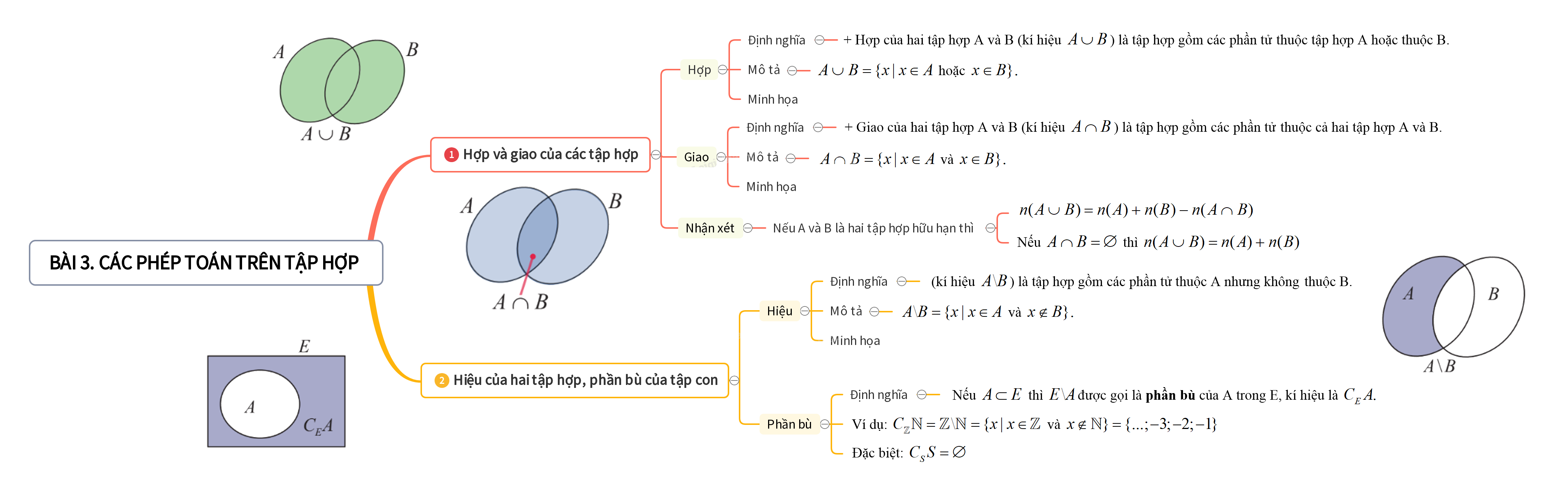
1. Hợp và giao của các tập hợp 2. Hiệu của hai tập hợp, phần bù của tập con
1. Hợp và giao của các tập hợp
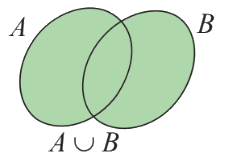
+ Hợp của hai tập hợp A và B (kí hiệu \(A \cup B\)) là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc T.
\(A \cup B = \{ x|x \in A\) hoặc \(x \in B\} .\)
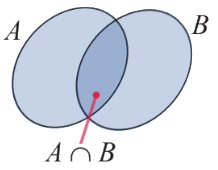
+ Giao của hai tập hợp A và B (kí hiệu \(A \cap B\)) là tập hợp gồm các phần tử thuộc cả hai tập hợp A và B.
\(A \cap B = \{ x|x \in A\) và \(x \in B\} .\)
+ Nhận xét: Nếu A và B là hai tập hợp hữu hạn thì
\(n(A \cup B) = n(A) + n(B) - n(A \cap B)\)
Nếu \(A \cap B = \emptyset \) thì \(n(A \cup B) = n(A) + n(B)\)
2. Hiệu của hai tập hợp, phần bù của tập con
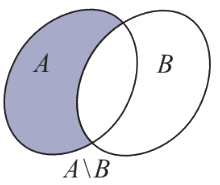
Hiệu của hai tập hợp A và B (kí hiệu \(A{\rm{\backslash }}B\)) là tập hợp gồm các phần tử thuộc A nhưng không thuộc B.
\(A{\rm{\backslash }}B = \{ x|x \in A\) và \(x \notin B\} .\)
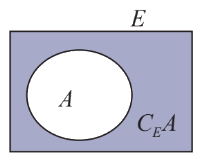
Nếu \(A \subset E\) thì \(E{\rm{\backslash }}A\)được gọi là phần bù của A trong E, kí hiệu là \({C_E}A.\)
Ví dụ: \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và \(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\} \)
Đặc biệt: \({C_S}S = \emptyset \)
Trong chương trình Toán 10 Chân trời sáng tạo, phần lý thuyết về các phép toán trên tập hợp đóng vai trò nền tảng cho việc hiểu và giải quyết các bài toán liên quan đến tập hợp. Bài viết này sẽ trình bày chi tiết lý thuyết này, bao gồm định nghĩa, tính chất và ví dụ minh họa.
Trước khi đi vào các phép toán, chúng ta cần nắm vững các khái niệm cơ bản về tập hợp:
Có bốn phép toán cơ bản trên tập hợp:
Các phép toán trên tập hợp có những tính chất quan trọng sau:
Xét A = {1, 2, 3} và B = {2, 4, 5}. Ta có:
Nếu tập hợp vũ trụ U = {1, 2, 3, 4, 5, 6}, thì A' = {4, 5, 6}
Các phép toán trên tập hợp có nhiều ứng dụng trong toán học và các lĩnh vực khác, ví dụ:
Để củng cố kiến thức, bạn có thể thực hành các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về lý thuyết các phép toán trên tập hợp trong chương trình Toán 10 Chân trời sáng tạo. Chúc bạn học tập tốt!