Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 61 và 62 sách giáo khoa Toán 10 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn Tìm các giá trị lượng giác của góc 135
Tìm các giá trị lượng giác của góc \({135^o}\)
Phương pháp giải:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\)
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {135^o},\;\sin {135^o}\)
Từ đó suy ra\(\;\tan {135^o} = \frac{{\sin {{135}^o}}}{{\cos {{135}^o}}},\;\;\cot {135^o} = \frac{{\cos {{135}^o}}}{{\sin {{135}^o}}}.\)
Lời giải chi tiết:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.
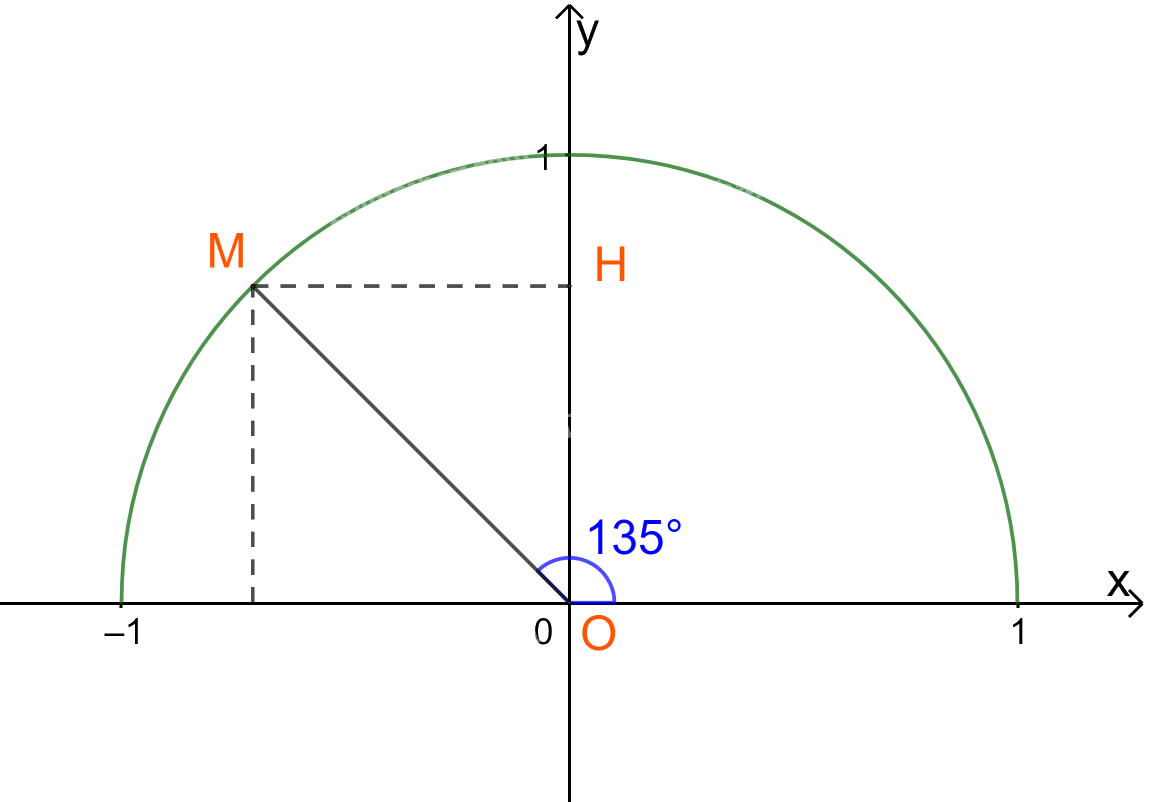
Ta có: \(\widehat {MOy} = {135^o} - {90^o} = {45^o}\).
Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)
Vậy tọa độ điểm M là \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)
Vậy theo định nghĩa ta có:
\(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} = - \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} = - 1;\;\;\cot {135^o} = - 1.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {135^o}\), bấm phím: sin 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\)
Tính \(\cos {135^o}\),bấm phím: cos 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{ - \sqrt 2 }}{2}\)
Tính \(\tan {135^o}\), bấm phím: tan 1 3 5 \(^o\)’’’ = ta được kết quả là \( - 1\)
(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\))
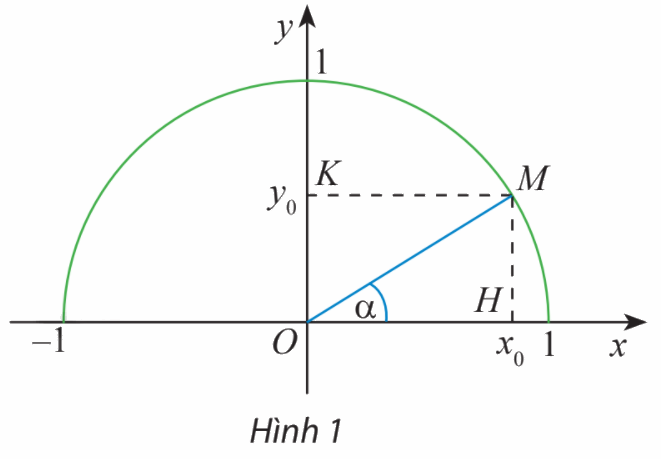
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
\(\sin \alpha = {y_0};\;\cos \alpha = {x_0};\;\tan \alpha = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{{x_0}}}{{{y_0}}}.\)
Phương pháp giải:
Tam giác vuông OHM có \(\alpha = \widehat {xOM}\)
\(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}};\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\)
Lời giải chi tiết:
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}}.\)
Mà \(MH = {y_0};OH = {x_0};OM = 1.\)
\( \Rightarrow \sin \alpha = \frac{{{y_0}}}{1} = {y_0};\;\cos \alpha = \frac{{{x_0}}}{1} = {x_0}\;.\)
\( \Rightarrow \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}.\)
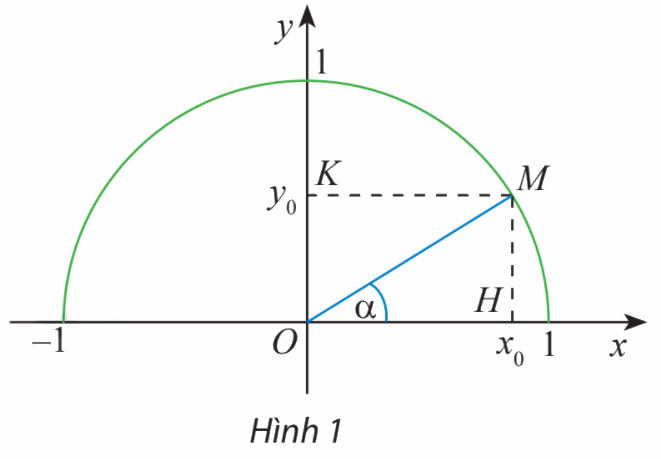
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
\(\sin \alpha = {y_0};\;\cos \alpha = {x_0};\;\tan \alpha = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{{x_0}}}{{{y_0}}}.\)
Phương pháp giải:
Tam giác vuông OHM có \(\alpha = \widehat {xOM}\)
\(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}};\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\)
Lời giải chi tiết:
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}};\;\cos \alpha = \frac{{OH}}{{OM}}.\)
Mà \(MH = {y_0};OH = {x_0};OM = 1.\)
\( \Rightarrow \sin \alpha = \frac{{{y_0}}}{1} = {y_0};\;\cos \alpha = \frac{{{x_0}}}{1} = {x_0}\;.\)
\( \Rightarrow \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}.\)
Tìm các giá trị lượng giác của góc \({135^o}\)
Phương pháp giải:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\)
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {135^o},\;\sin {135^o}\)
Từ đó suy ra\(\;\tan {135^o} = \frac{{\sin {{135}^o}}}{{\cos {{135}^o}}},\;\;\cot {135^o} = \frac{{\cos {{135}^o}}}{{\sin {{135}^o}}}.\)
Lời giải chi tiết:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.
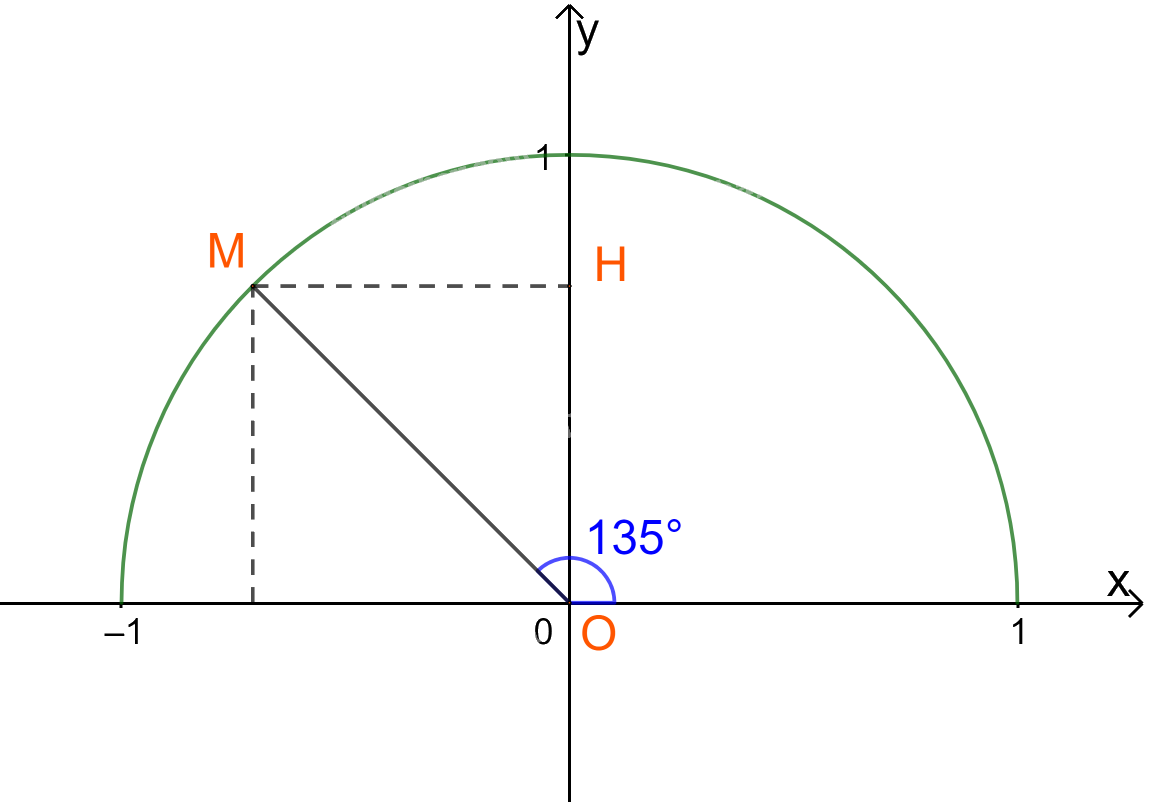
Ta có: \(\widehat {MOy} = {135^o} - {90^o} = {45^o}\).
Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)
Vậy tọa độ điểm M là \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)
Vậy theo định nghĩa ta có:
\(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} = - \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} = - 1;\;\;\cot {135^o} = - 1.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {135^o}\), bấm phím: sin 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\)
Tính \(\cos {135^o}\),bấm phím: cos 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{ - \sqrt 2 }}{2}\)
Tính \(\tan {135^o}\), bấm phím: tan 1 3 5 \(^o\)’’’ = ta được kết quả là \( - 1\)
(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\))
Mục 1 của chương trình Toán 10 tập 1, Chân trời sáng tạo tập trung vào việc giới thiệu các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp và các tính chất của chúng. Đây là nền tảng quan trọng để học sinh có thể tiếp cận các kiến thức phức tạp hơn trong các chương tiếp theo.
Tập hợp là một khái niệm nền tảng trong toán học. Một tập hợp là một sưu tập các đối tượng được xác định rõ ràng. Các đối tượng này được gọi là các phần tử của tập hợp. Ví dụ, tập hợp các số tự nhiên, tập hợp các số nguyên, tập hợp các số thực, v.v.
Có một số phép toán cơ bản trên tập hợp, bao gồm:
Dưới đây là một số bài tập minh họa và lời giải chi tiết cho các bài tập trong mục 1 trang 61, 62 SGK Toán 10 tập 1 - Chân trời sáng tạo:
Lời giải:
Lời giải:
Để giải bài tập về tập hợp một cách hiệu quả, các em cần lưu ý những điều sau:
Tập hợp có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức hữu ích về giải mục 1 trang 61, 62 SGK Toán 10 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!