Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 33, 34 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục này tập trung vào các kiến thức cơ bản về tập hợp, các phép toán trên tập hợp và biểu diễn tập hợp.
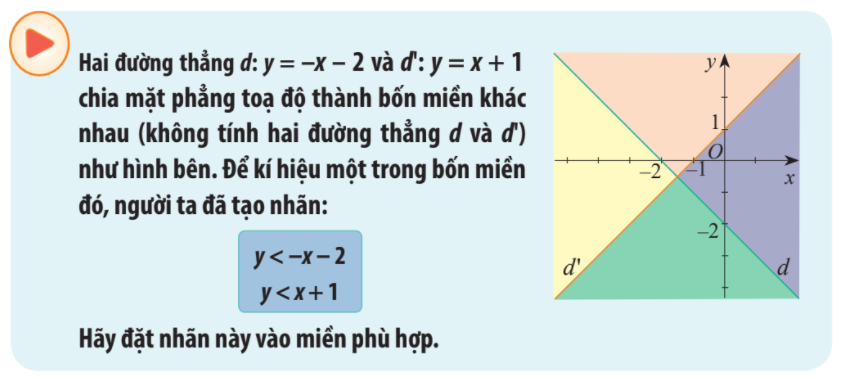
Hãy đặt nhãn vào miền phù hợp Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.
Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua.
Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng.
a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.
b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên?
(20; 40), (40; 20), (-30; 10).
Lời giải chi tiết:
a)
Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)
Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)
Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)
Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)
b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).
+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).
+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).
Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.
Lời giải chi tiết:
a) \(\left\{ \begin{array}{l}3x + y - 1 \le 0\\2x - y + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + 0 - 1 = - 1 \le 0\\2.0 - 0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((0; - 1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + ( - 1) - 1 = - 2 \le 0\\2.0 - ( - 1) + 2 = 3 \ge 0\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y - 1 < 0\\x + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((1;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\1 + 2 = 3 \ge 0\end{array} \right.\)
d) \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 0 - 3 = - 3 \le 0\\ - 2.0 + 0 + 3 = 3 \ge 0\\0 \ge 0\\0 \ge 0\end{array} \right.\)
Cặp số \((0;1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 1 - 3 = - 2 \le 0\\ - 2.0 + 1 + 3 = 4 \ge 0\\0 \ge 0\\1 \ge 0\end{array} \right.\)
Lời giải chi tiết:
Vì \(0 > - 0 - 2\) nên điểm O(0;0) không thuộc miền nghiệm của bất phương trình \(y < - x - 2\)
Miền nghiệm của BPT \(y < - x - 2\) là miền được tô màu vàng và xanh.
Vì \(0 < 0 + 1\) nên điểm O(0;0) thuộc miền nghiệm của bất phương trình \(y < x + 1\)
Miền nghiệm của BPT \(y < x + 1\) là miền được tô màu xanh và tím.
Vậy miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y < - x - 2\\y < x + 1\end{array} \right.\) là miền màu xanh (không kể các bờ d, d’)
Nói cách khác nhãn đã cho là nhãn của miền màu xanh.
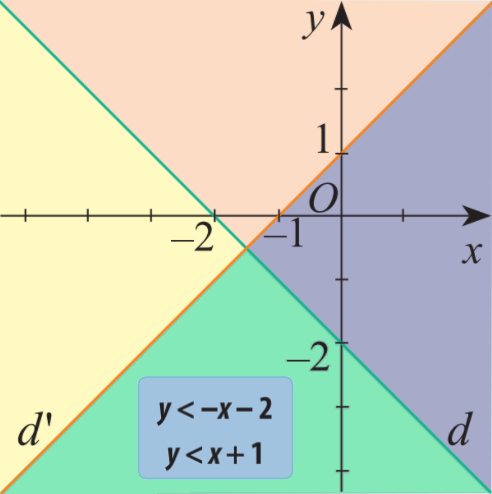
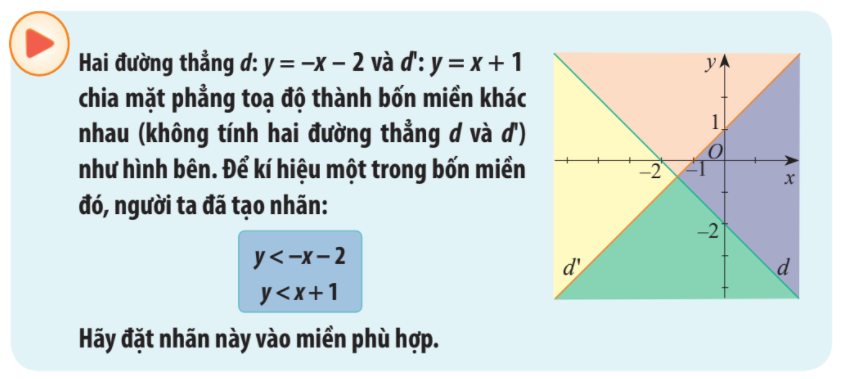
Lời giải chi tiết:
Vì \(0 > - 0 - 2\) nên điểm O(0;0) không thuộc miền nghiệm của bất phương trình \(y < - x - 2\)
Miền nghiệm của BPT \(y < - x - 2\) là miền được tô màu vàng và xanh.
Vì \(0 < 0 + 1\) nên điểm O(0;0) thuộc miền nghiệm của bất phương trình \(y < x + 1\)
Miền nghiệm của BPT \(y < x + 1\) là miền được tô màu xanh và tím.
Vậy miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y < - x - 2\\y < x + 1\end{array} \right.\) là miền màu xanh (không kể các bờ d, d’)
Nói cách khác nhãn đã cho là nhãn của miền màu xanh.
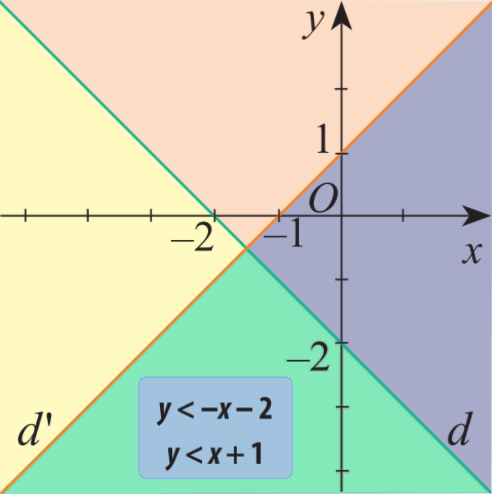
Một người nông dân dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua.
Biết rằng người đó chỉ có tối đa 9 triệu đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng cà tím là 200 000 đồng, mỗi sào đất trồng cà chua là 100 000 đồng.
a) Viết các bất phương trình mô tả các điều kiện ràng buộc đối với x, y.
b) Cặp số nào sau đây thỏa mãn đồng thời tất cả các bất phương trình nêu trên?
(20; 40), (40; 20), (-30; 10).
Lời giải chi tiết:
a)
Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)
Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)
Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)
Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)
b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).
+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).
+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).
Hãy chỉ ra hai nghiệm của mỗi hệ bất phương trình trong Ví dụ 1.
Lời giải chi tiết:
a) \(\left\{ \begin{array}{l}3x + y - 1 \le 0\\2x - y + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + 0 - 1 = - 1 \le 0\\2.0 - 0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((0; - 1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}3.0 + ( - 1) - 1 = - 2 \le 0\\2.0 - ( - 1) + 2 = 3 \ge 0\end{array} \right.\)
c) \(\left\{ \begin{array}{l}y - 1 < 0\\x + 2 \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\0 + 2 = 2 \ge 0\end{array} \right.\)
Cặp số \((1;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 - 1 = - 1 < 0\\1 + 2 = 3 \ge 0\end{array} \right.\)
d) \(\left\{ \begin{array}{l}x + y - 3 \le 0\\ - 2x + y + 3 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Cặp số \((0;0)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 0 - 3 = - 3 \le 0\\ - 2.0 + 0 + 3 = 3 \ge 0\\0 \ge 0\\0 \ge 0\end{array} \right.\)
Cặp số \((0;1)\) là một nghiệm của hệ bất phương trình trên vì \(\left\{ \begin{array}{l}0 + 1 - 3 = - 2 \le 0\\ - 2.0 + 1 + 3 = 4 \ge 0\\0 \ge 0\\1 \ge 0\end{array} \right.\)
Mục 1 của chương trình Toán 10 tập 1 Chân trời sáng tạo giới thiệu những khái niệm cơ bản về tập hợp, một trong những nền tảng quan trọng của toán học. Việc nắm vững kiến thức về tập hợp là bước đệm cần thiết để học tốt các chương trình toán học nâng cao hơn. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trang 33 và 34, đồng thời phân tích phương pháp giải để giúp học sinh hiểu rõ bản chất của vấn đề.
Tập hợp là một khái niệm cơ bản trong toán học, dùng để chứa các đối tượng được xác định rõ ràng. Các đối tượng này được gọi là các phần tử của tập hợp. Để hiểu rõ hơn về tập hợp, chúng ta cần nắm vững các khái niệm sau:
Các phép toán trên tập hợp cho phép chúng ta tạo ra các tập hợp mới từ các tập hợp đã cho. Các phép toán phổ biến bao gồm:
Dưới đây là lời giải chi tiết cho các bài tập mục 1 trang 33 và 34 SGK Toán 10 tập 1 Chân trời sáng tạo:
Liệt kê các phần tử của các tập hợp sau:
Lời giải:
Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm:
Lời giải:
Để củng cố kiến thức về tập hợp, các em có thể thực hành thêm các bài tập sau:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích và phương pháp giải bài tập hiệu quả. Chúc các em học tập tốt!