Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB
Đề bài
Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB
Phương pháp giải - Xem chi tiết
Bước 1: Xét với đường tròn bất kì, cho tọa độ các điểm A, B, C, D
Bước 2: Xác định tọa độ điểm E, F
Bước 3: Tính \(\overrightarrow {EF} .\overrightarrow {DB} \), suy ra vuông góc
Lời giải chi tiết
Xét với đường tròn (O) có phương trình \((O):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 25\)
Cho các điểm \(A(0;0),B(0;8),C(8;4),D( - 2;4)\) nằm trên đường tròn (O) và thỏa mãn AB vuông góc với CD
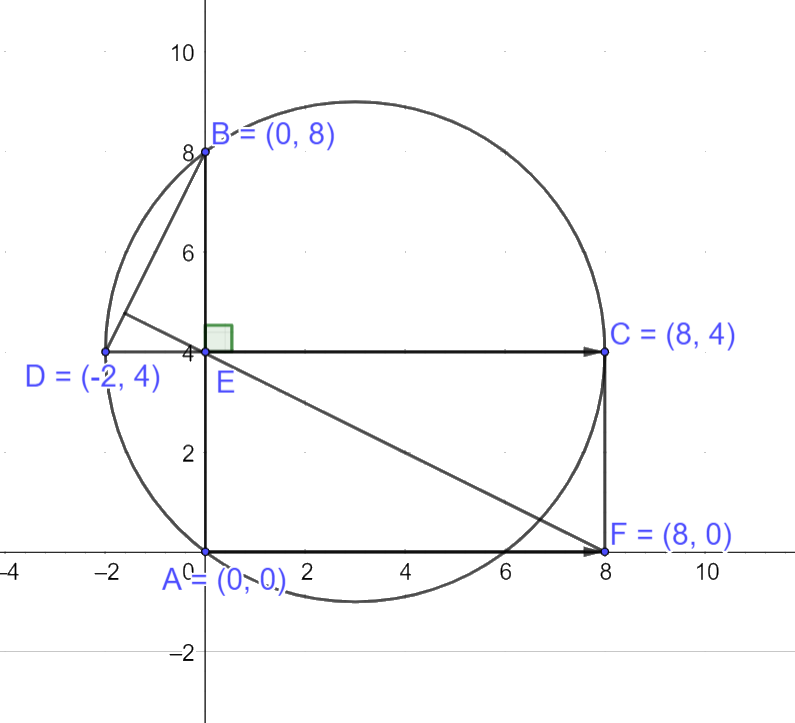
Phương trình đường thẳng đi qua hai điểm A, B có dạng \(x = 0\)
Phương trình đường thẳng đi qua hai điểm C, D có dạng \(y = 4\)
Ta có AB vuông góc với CD tại điểm E nên tọa độ điểm E là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}x = 0\\y = 4\end{array} \right. \Leftrightarrow E(0;4)\)
Gọi tọa độ của điểm F là: \(F(x;y)\)
ACEF là hình chữ nhật nên \(\overrightarrow {AF} = \overrightarrow {EC} \), mặt khác ta có: \(\overrightarrow {AF} = (x;y),\overrightarrow {EC} = \left( {8;0} \right)\)
Suy ra tọa độ điểm F là: \(F\left( {8;0} \right)\)
\(\overrightarrow {EF} = \left( {8; - 4} \right),\overrightarrow {DB} = \left( {2;4} \right) \Rightarrow \overrightarrow {EF} .\overrightarrow {BD} = 8.2 + \left( { - 4} \right).4 = 0 \Rightarrow \overrightarrow {EF} \bot \overrightarrow {BD} \)
Vậy ta chứng minh được EF vuông góc với DB
Bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của chúng.
Bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập.
Giả sử cho hai điểm A(xA, yA, zA) và B(xB, yB, zB). Vectơ AB có tọa độ là:
AB = (xB - xA, yB - yA, zB - zA)
Ví dụ: Cho A(1, 2, 3) và B(4, 5, 6). Khi đó, vectơ AB có tọa độ là:
AB = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3)
Cho hai vectơ a = (x1, y1, z1) và b = (x2, y2, z2). Khi đó:
Ví dụ: Cho a = (1, 2, 3) và b = (4, 5, 6). Khi đó:
a + b = (1 + 4, 2 + 5, 3 + 6) = (5, 7, 9)
a - b = (1 - 4, 2 - 5, 3 - 6) = (-3, -3, -3)
2.a = (2.1, 2.2, 2.3) = (2, 4, 6)
Để chứng minh đẳng thức vectơ, ta có thể sử dụng các tính chất của vectơ như tính giao hoán, tính kết hợp, tính chất phân phối, và các quy tắc biến đổi vectơ.
Ví dụ: Chứng minh rằng a + b = b + a. Ta có:
a + b = (x1 + x2, y1 + y2, z1 + z2) = (x2 + x1, y2 + y1, z2 + z1) = b + a
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các bạn học sinh sẽ tự tin hơn trong việc giải bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạo. Chúc các bạn học tập tốt!