Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Toán 10 Chân trời sáng tạo, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 10 tập 1 tập trung vào các khái niệm và bài tập về tập hợp, các phép toán trên tập hợp, và các ứng dụng của tập hợp trong thực tế.
Tìm tập xác định của các hàm số sau: Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y=-x^2 trên Hình 2 Vẽ đồ thị hàm số y = x^2 - 4x + 3 rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0), quay xuống dưới nếu a<0.
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\) là một parabol (P1):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
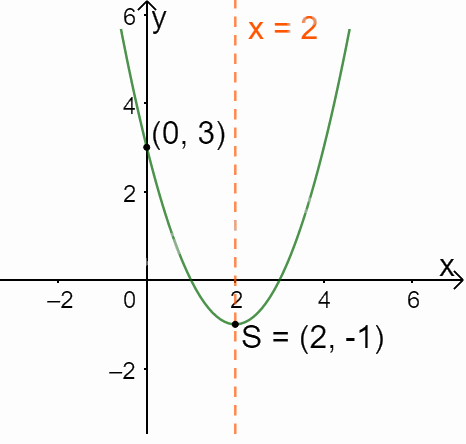
*So sánh với đồ thị hàm số ở Ví dụ 2a:
Giống nhau: Có chung trục đối xứng
Khác nhau:
Điểm đỉnh và giao điểm với trục tung của hai hàm số đối xứng với nhau qua trục Ox.
Bề lõm của (P) xuống dưới còn (P1) quay lên trên.
Nhận xét chung: Hai đồ thị này đối xứng với nhau qua trục Ox.
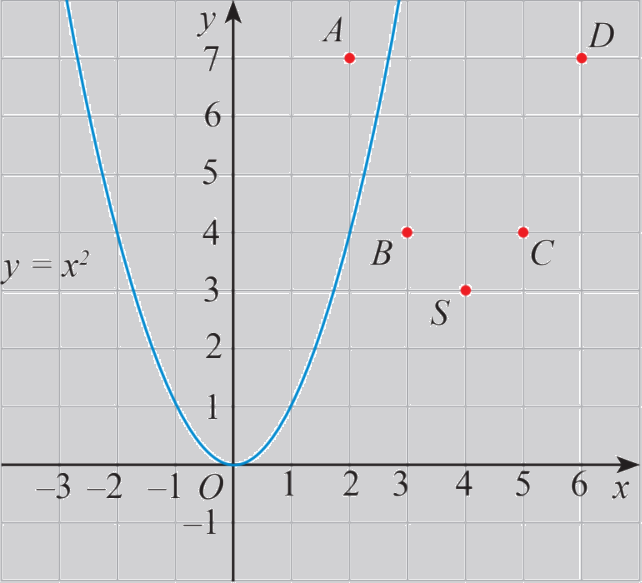
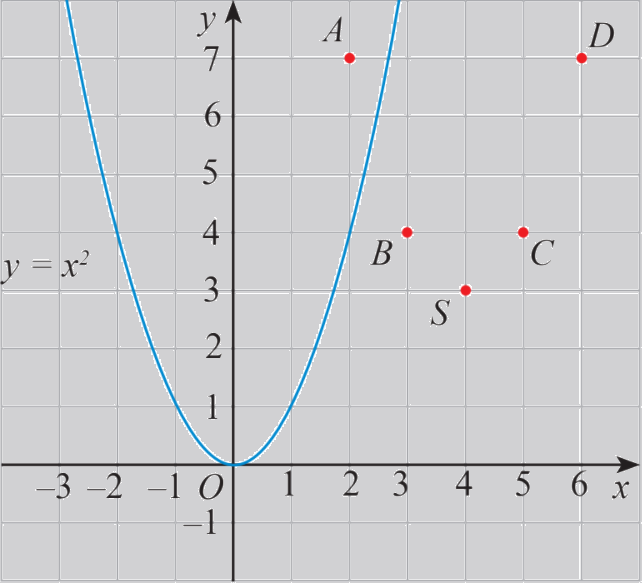
a) Xét hàm số\(y = f(x) = {x^2} - 8x + 19 = {(x - 4)^2} + 3\) có bảng giá trị:
\(x\) | 2 | 3 | 4 | 5 | 6 |
\(f(x)\) | 7 | 4 | 3 | 4 | 7 |
Trên mặt phẳng tọa độ, ta có các điểm \((x;f(x))\) với x thuộc bảng giá trị đã cho (hình 1).
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số \(y = {x^2}\) trên Hình 1.
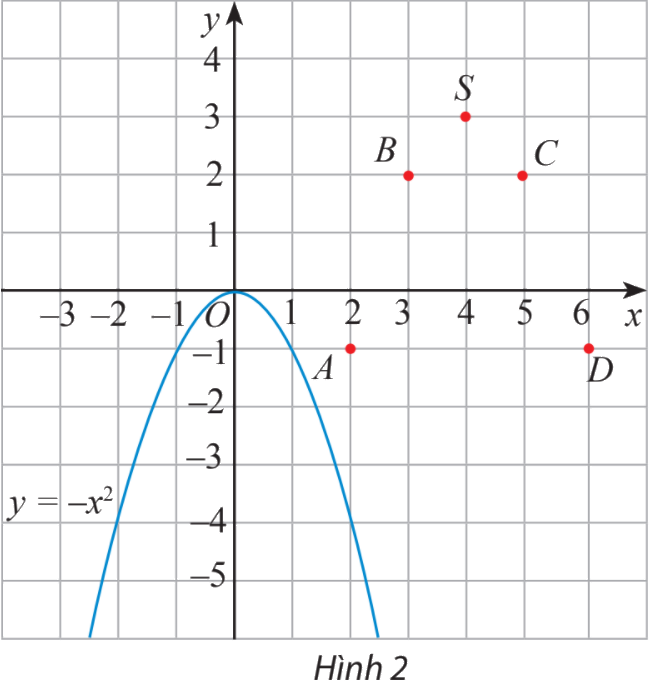
b) Tương tự xét hàm số \(y = g(x) = - {x^2} + 8x - 13 = - {(x - 4)^2} + 3\) có bảng giá trị:
\(x\) | 2 | 3 | 4 | 5 | 6 |
\(f(x)\) | -1 | 2 | 3 | 2 | -1 |
Trên mặt phẳng tọa độ, ta có các điểm \((x;f(x))\) với x thuộc bảng giá trị đã cho (hình 2).
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số \(y = - {x^2}\) trên Hình 2.
Lời giải chi tiết:
a)
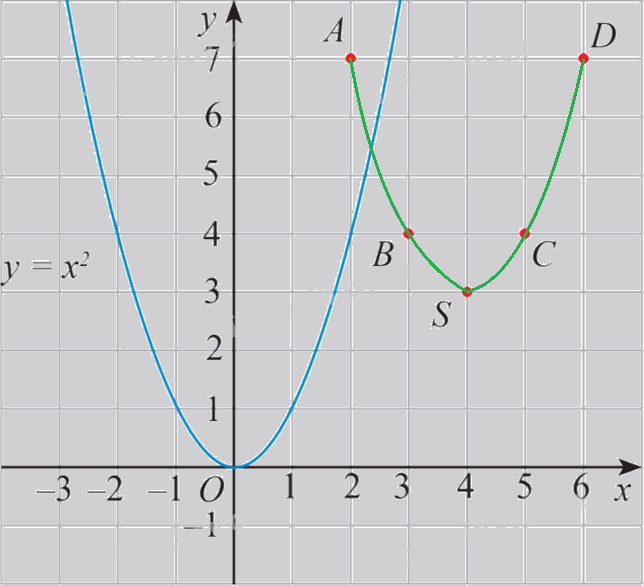
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số \(y = {x^2}\), cùng có bề lõm quay lên trên.
b)
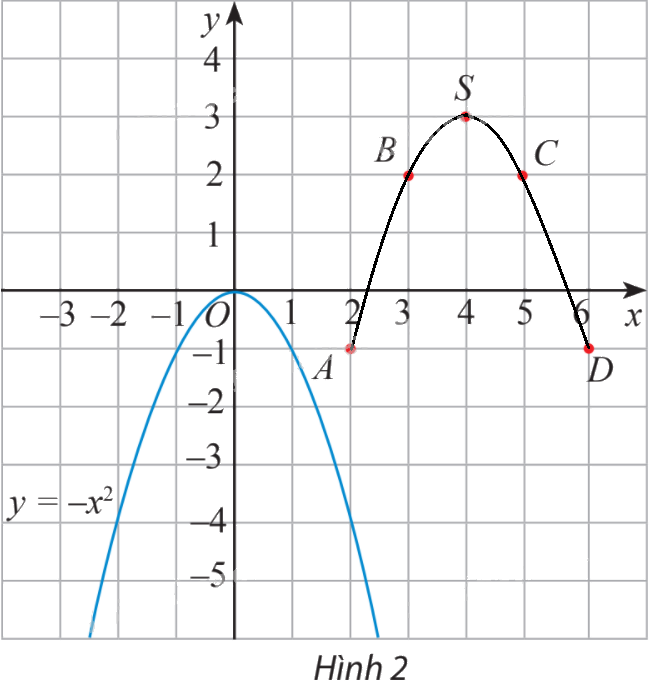
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số \(y = - {x^2}\), cùng có bề lõm quay xuống dưới.
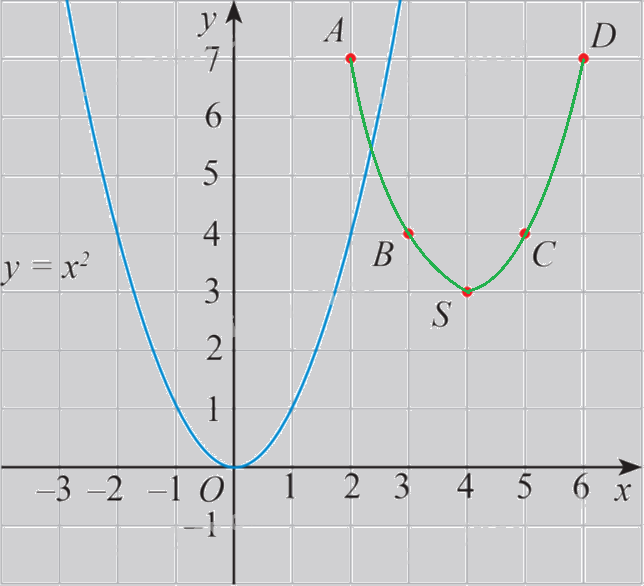
a) Xét hàm số\(y = f(x) = {x^2} - 8x + 19 = {(x - 4)^2} + 3\) có bảng giá trị:
\(x\) | 2 | 3 | 4 | 5 | 6 |
\(f(x)\) | 7 | 4 | 3 | 4 | 7 |
Trên mặt phẳng tọa độ, ta có các điểm \((x;f(x))\) với x thuộc bảng giá trị đã cho (hình 1).
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số \(y = {x^2}\) trên Hình 1.
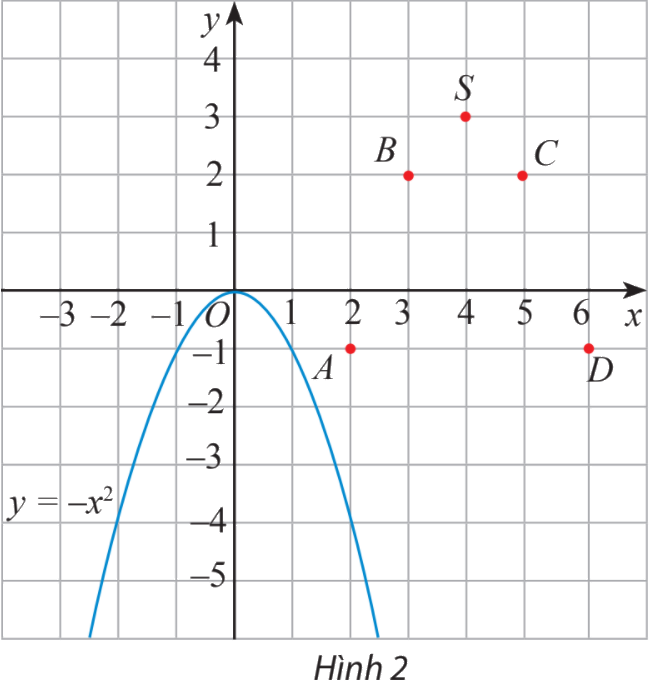
b) Tương tự xét hàm số \(y = g(x) = - {x^2} + 8x - 13 = - {(x - 4)^2} + 3\) có bảng giá trị:
\(x\) | 2 | 3 | 4 | 5 | 6 |
\(f(x)\) | -1 | 2 | 3 | 2 | -1 |
Trên mặt phẳng tọa độ, ta có các điểm \((x;f(x))\) với x thuộc bảng giá trị đã cho (hình 2).
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số \(y = - {x^2}\) trên Hình 2.
Lời giải chi tiết:
a)
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số \(y = {x^2}\), cùng có bề lõm quay lên trên.
b)
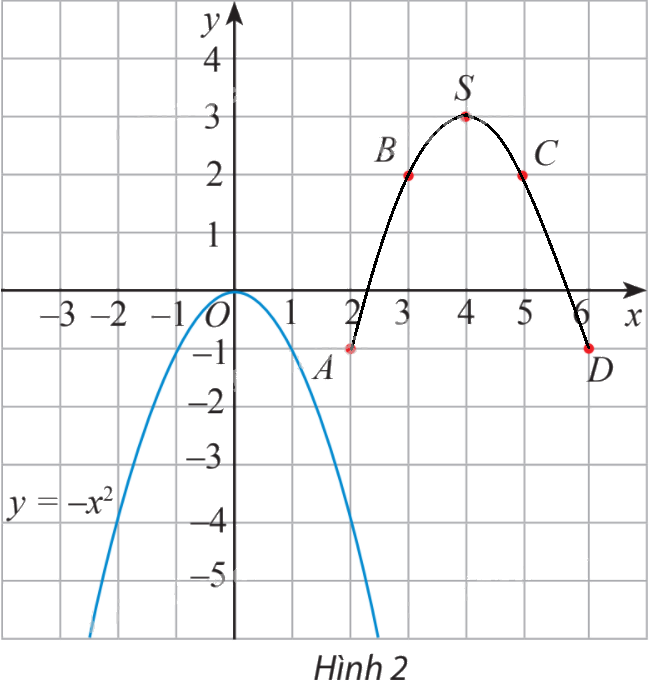
Đường cong đi qua 5 điểm này có cùng hình dạng với đồ thị hàm số \(y = - {x^2}\), cùng có bề lõm quay xuống dưới.
Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Phương pháp giải:
+ Xác định đỉnh \(S(\frac{{ - b}}{{2a}};f(\frac{{ - b}}{{2a}}))\)
+ Trục đối xứng \(x = \frac{{ - b}}{{2a}}\)
+ Bề lõm: quay lên trên (nếu a>0), quay xuống dưới nếu a<0.
+ Giao với trục tung tại điểm có tọa độ (0; c).
Lời giải chi tiết:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\) là một parabol (P1):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
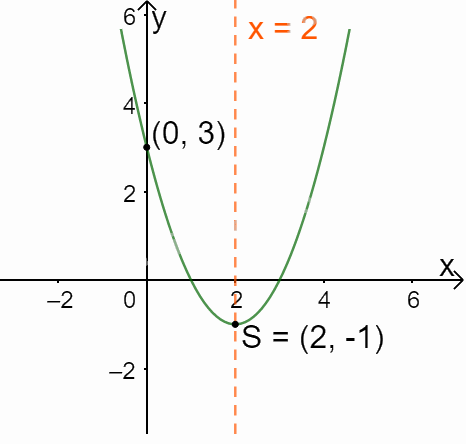
*So sánh với đồ thị hàm số ở Ví dụ 2a:
Giống nhau: Có chung trục đối xứng
Khác nhau:
Điểm đỉnh và giao điểm với trục tung của hai hàm số đối xứng với nhau qua trục Ox.
Bề lõm của (P) xuống dưới còn (P1) quay lên trên.
Nhận xét chung: Hai đồ thị này đối xứng với nhau qua trục Ox.
Mục 2 trong SGK Toán 10 tập 1 Chân trời sáng tạo là một phần quan trọng, đặt nền móng cho các kiến thức toán học nâng cao hơn. Nội dung chính của mục này xoay quanh các khái niệm cơ bản về tập hợp, bao gồm định nghĩa tập hợp, các ký hiệu, cách biểu diễn tập hợp, và các phép toán trên tập hợp như hợp, giao, hiệu, phần bù. Việc nắm vững các khái niệm này là điều kiện cần thiết để giải quyết các bài toán liên quan đến tập hợp một cách hiệu quả.
Các bài tập trên trang 49 tập trung vào việc rèn luyện kỹ năng xác định một tập hợp dựa trên các tiêu chí cho trước, và xác định xem một phần tử có thuộc một tập hợp hay không. Các em cần nắm vững định nghĩa tập hợp và hiểu rõ ý nghĩa của các ký hiệu toán học để giải quyết các bài tập này.
Trang 50 giới thiệu các phép toán cơ bản trên tập hợp: hợp (union), giao (intersection), hiệu (difference). Các bài tập yêu cầu các em thực hiện các phép toán này trên các tập hợp cụ thể, và hiểu rõ ý nghĩa của kết quả. Việc sử dụng sơ đồ Venn có thể giúp các em hình dung rõ hơn về các phép toán này.
Phần bù của một tập hợp là tập hợp tất cả các phần tử thuộc tập hợp vũ trụ nhưng không thuộc tập hợp ban đầu. Các bài tập trên trang 51 yêu cầu các em xác định phần bù của một tập hợp trong một tập hợp vũ trụ cho trước. Điều quan trọng là các em phải xác định rõ tập hợp vũ trụ trước khi tính toán phần bù.
Trang 52 chứa các bài tập tổng hợp, kết hợp các kiến thức và kỹ năng đã học ở các trang trước. Các bài tập này thường có tính ứng dụng cao, yêu cầu các em áp dụng kiến thức về tập hợp để giải quyết các vấn đề thực tế. Ví dụ, các em có thể sử dụng tập hợp để mô tả các nhóm đối tượng khác nhau, hoặc để phân tích dữ liệu.
Bài tập: Cho A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B và A ∩ B.
Giải:
Để học tốt môn Toán 10, các em cần dành thời gian ôn tập lý thuyết, làm bài tập thường xuyên, và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
| Phép toán | Ký hiệu | Định nghĩa |
|---|---|---|
| Hợp | ∪ | Tập hợp chứa tất cả các phần tử thuộc A hoặc B |
| Giao | ∩ | Tập hợp chứa tất cả các phần tử thuộc cả A và B |
| Hiệu | \ | Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B |
| Phần bù | CA | Tập hợp chứa tất cả các phần tử thuộc tập hợp vũ trụ nhưng không thuộc A |