Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 94, 95 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 1 trang 94, 95 tập trung vào các kiến thức cơ bản về tập hợp, các phép toán trên tập hợp và ứng dụng của chúng.
Hãy xác định độ dài và hướng của hai vectơ Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ.
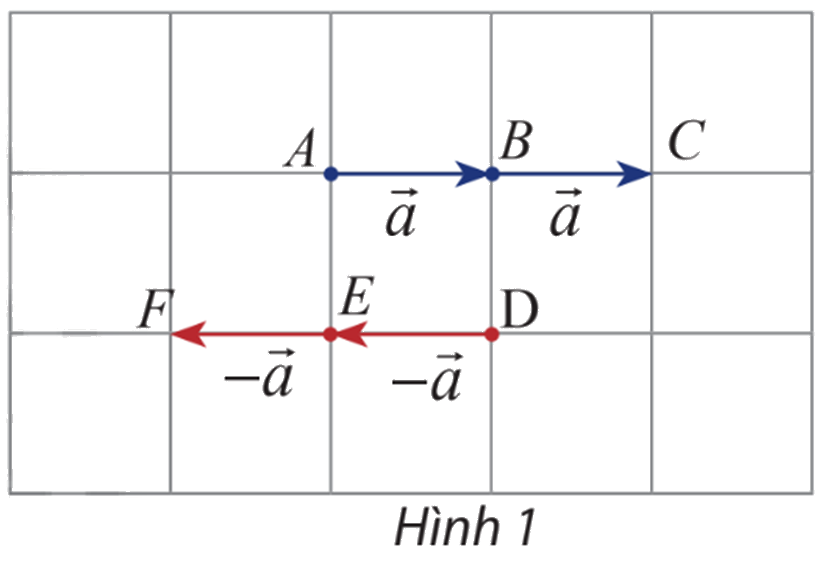
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)
Lời giải chi tiết:
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Phương pháp giải:
Sử dụng quy tắc 3 điểm \(\overrightarrow {MA} = \overrightarrow {MG} + \overrightarrow {GA}\)
Lời giải chi tiết:
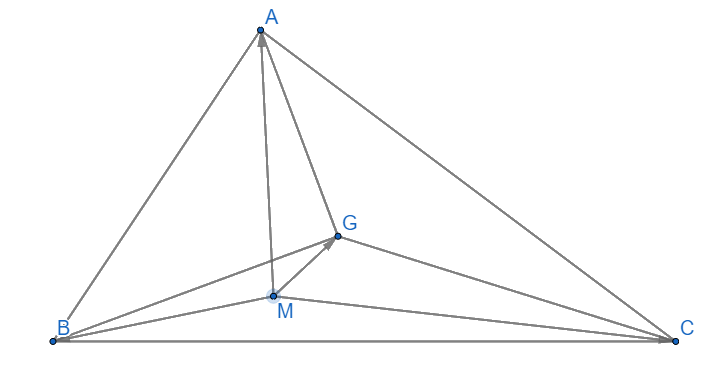
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \Leftrightarrow \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} = 3\overrightarrow {MG} \)
\( \Leftrightarrow \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG} \)
\( \Leftrightarrow 3\overrightarrow {MG} = 3\overrightarrow {MG} \) (đpcm) ( Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \))
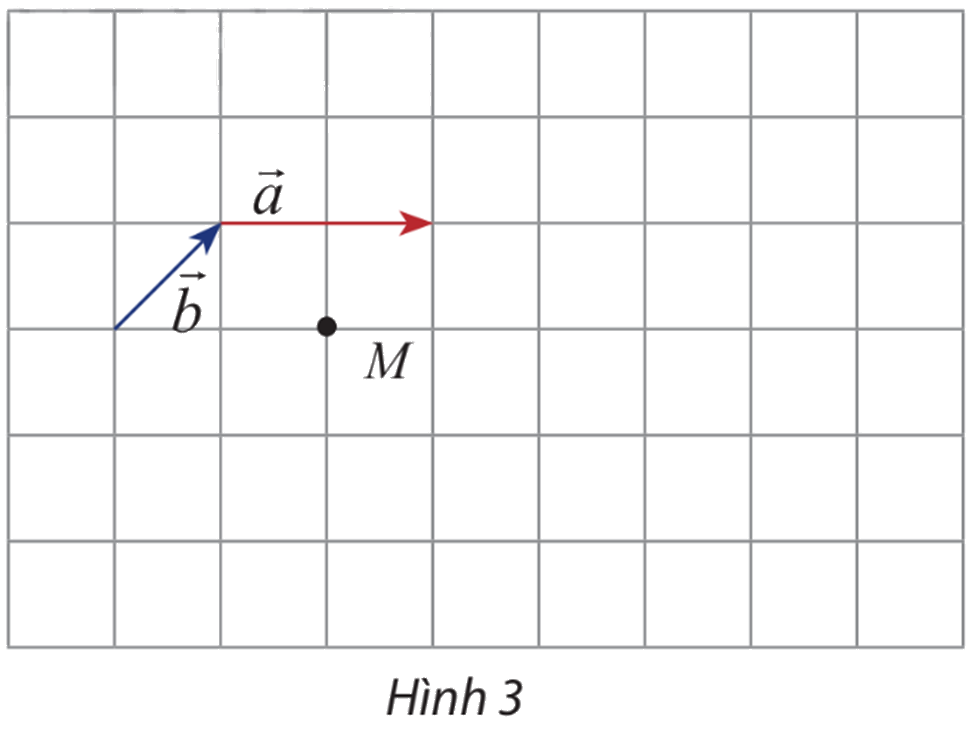
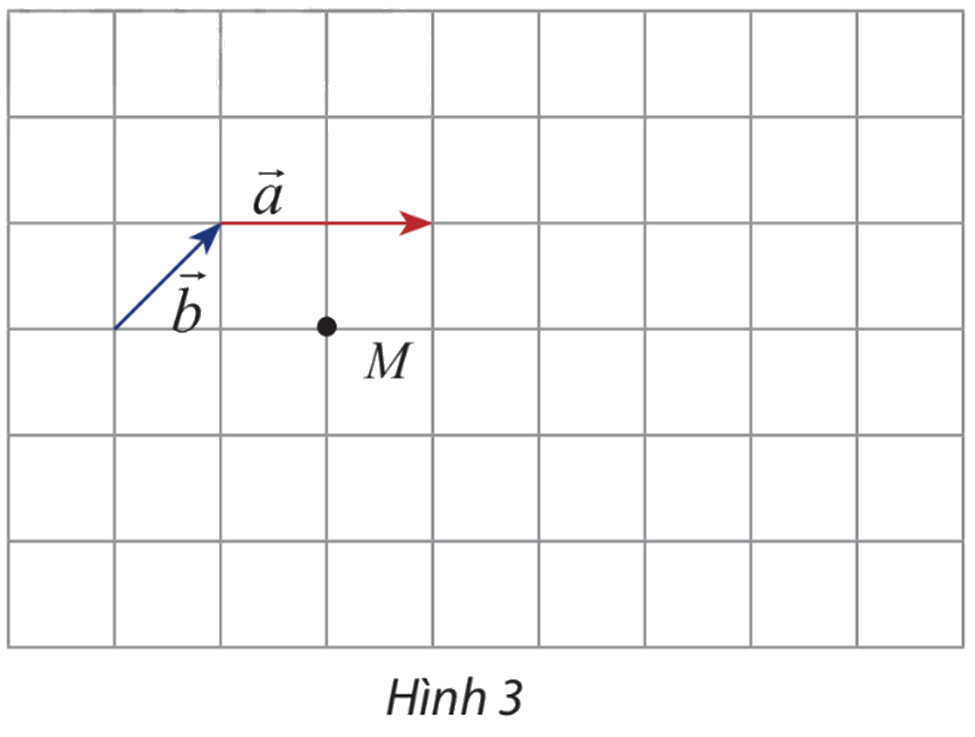
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
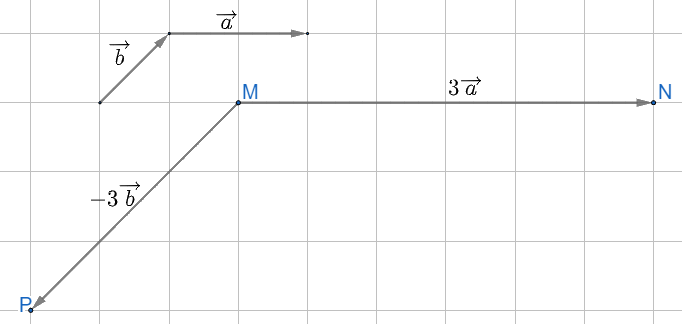
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).
Phương pháp giải:
Bước 1: Xác định hướng của vectơ \(\overrightarrow a ;\overrightarrow b \)
Bước 2: Xác định tỉ lệ độ dài \(\frac{{\left| {\overrightarrow x } \right|}}{{\left| {\overrightarrow a } \right|}}\)
Lời giải chi tiết:
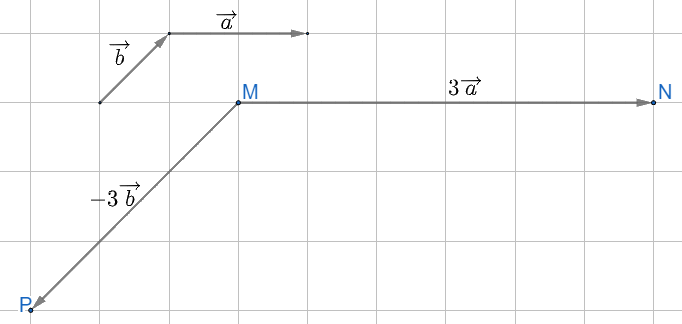
a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)
Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lý/giờ. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của tàu B theo vectơ vận tốc \(\overrightarrow a \) của tòa A.
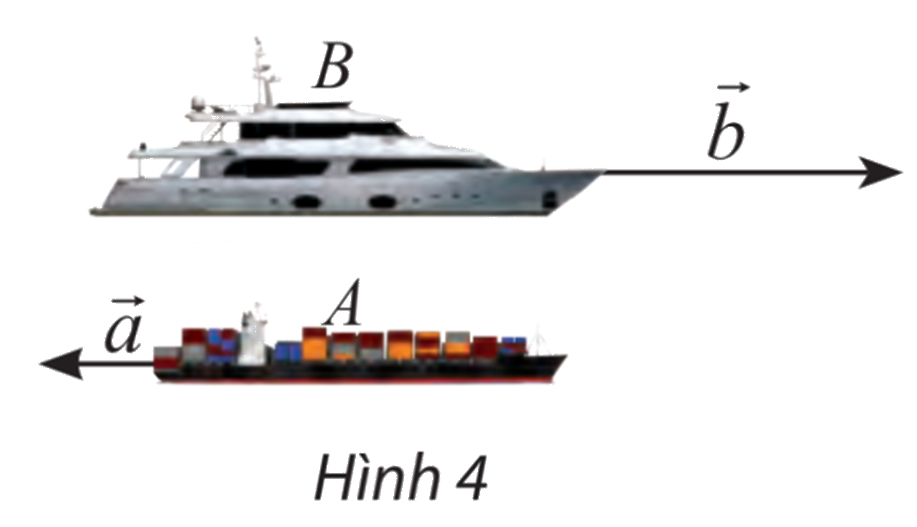
Lời giải chi tiết:
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)

Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)

Lời giải chi tiết:
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).
Phương pháp giải:
Bước 1: Xác định hướng của vectơ \(\overrightarrow a ;\overrightarrow b \)
Bước 2: Xác định tỉ lệ độ dài \(\frac{{\left| {\overrightarrow x } \right|}}{{\left| {\overrightarrow a } \right|}}\)
Lời giải chi tiết:
a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)
Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Phương pháp giải:
Sử dụng quy tắc 3 điểm \(\overrightarrow {MA} = \overrightarrow {MG} + \overrightarrow {GA}\)
Lời giải chi tiết:
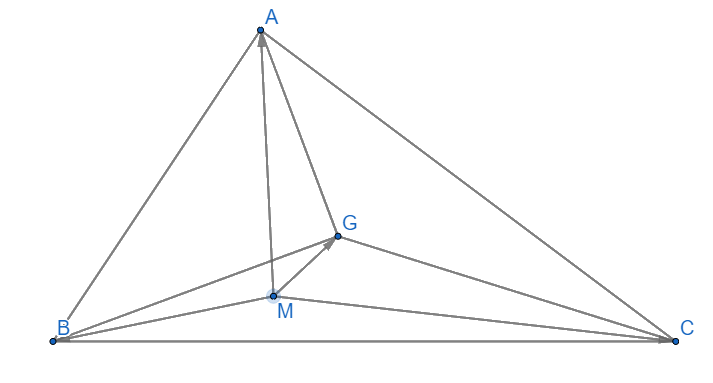
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \Leftrightarrow \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} = 3\overrightarrow {MG} \)
\( \Leftrightarrow \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG} \)
\( \Leftrightarrow 3\overrightarrow {MG} = 3\overrightarrow {MG} \) (đpcm) ( Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \))
Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lý/giờ. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của tàu B theo vectơ vận tốc \(\overrightarrow a \) của tòa A.
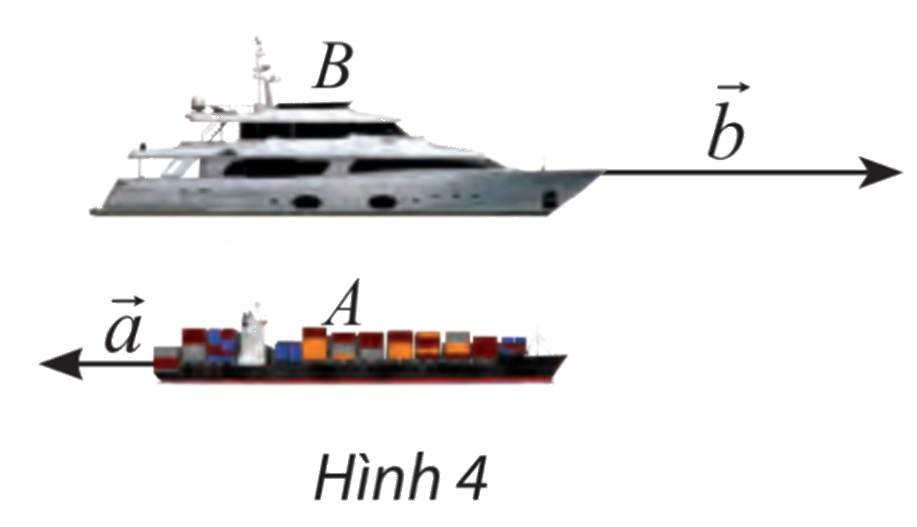
Lời giải chi tiết:
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)

Mục 1 của chương trình Toán 10 tập 1 Chân trời sáng tạo giới thiệu về khái niệm tập hợp, các loại tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, bù) và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Dưới đây là lời giải chi tiết các bài tập trang 94 SGK Toán 10 tập 1 Chân trời sáng tạo:
Bài tập yêu cầu xác định các tập hợp dựa trên các điều kiện cho trước. Ví dụ, xác định tập hợp các số tự nhiên chẵn nhỏ hơn 10. Để giải bài tập này, cần hiểu rõ định nghĩa của tập hợp và cách liệt kê các phần tử thuộc tập hợp.
Bài tập yêu cầu thực hiện các phép toán hợp, giao, hiệu, bù trên các tập hợp cho trước. Ví dụ, cho A = {1, 2, 3} và B = {2, 3, 4}, hãy tìm A ∪ B, A ∩ B, A \ B.
Để giải bài tập này, cần nắm vững định nghĩa và quy tắc thực hiện các phép toán trên tập hợp.
Các bài tập trang 95 thường tập trung vào việc vận dụng các kiến thức về tập hợp để giải quyết các bài toán phức tạp hơn. Ví dụ, chứng minh các đẳng thức liên quan đến phép toán trên tập hợp.
Bài tập yêu cầu chứng minh một đẳng thức liên quan đến các phép toán trên tập hợp. Ví dụ, chứng minh A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Để giải bài tập này, cần sử dụng các tính chất của phép toán trên tập hợp và các quy tắc logic.
Bài tập yêu cầu sử dụng kiến thức về tập hợp để giải quyết một bài toán thực tế. Ví dụ, một lớp học có 30 học sinh, trong đó có 15 học sinh thích môn Toán, 10 học sinh thích môn Văn, 5 học sinh thích cả hai môn. Hỏi có bao nhiêu học sinh không thích môn Toán và không thích môn Văn?
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 94, 95 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!