Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 30, 31, 32 sách giáo khoa Toán 10 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Cho bất phương trình 2x - y + 1 < 0 Biểu diễn miền nghiệm của các bất phương trình sau: Biểu diễn miền nghiệm của hai bất phương trình sau trên cùng mặt phẳng tọa độ Oxy
Biểu diễn miền nghiệm của hai bất phương trình sau trên cùng một mặt phẳng tọa độ Oxy:
a) \(y \ge 2\)
b) \(x \le 4\)
Lời giải chi tiết:
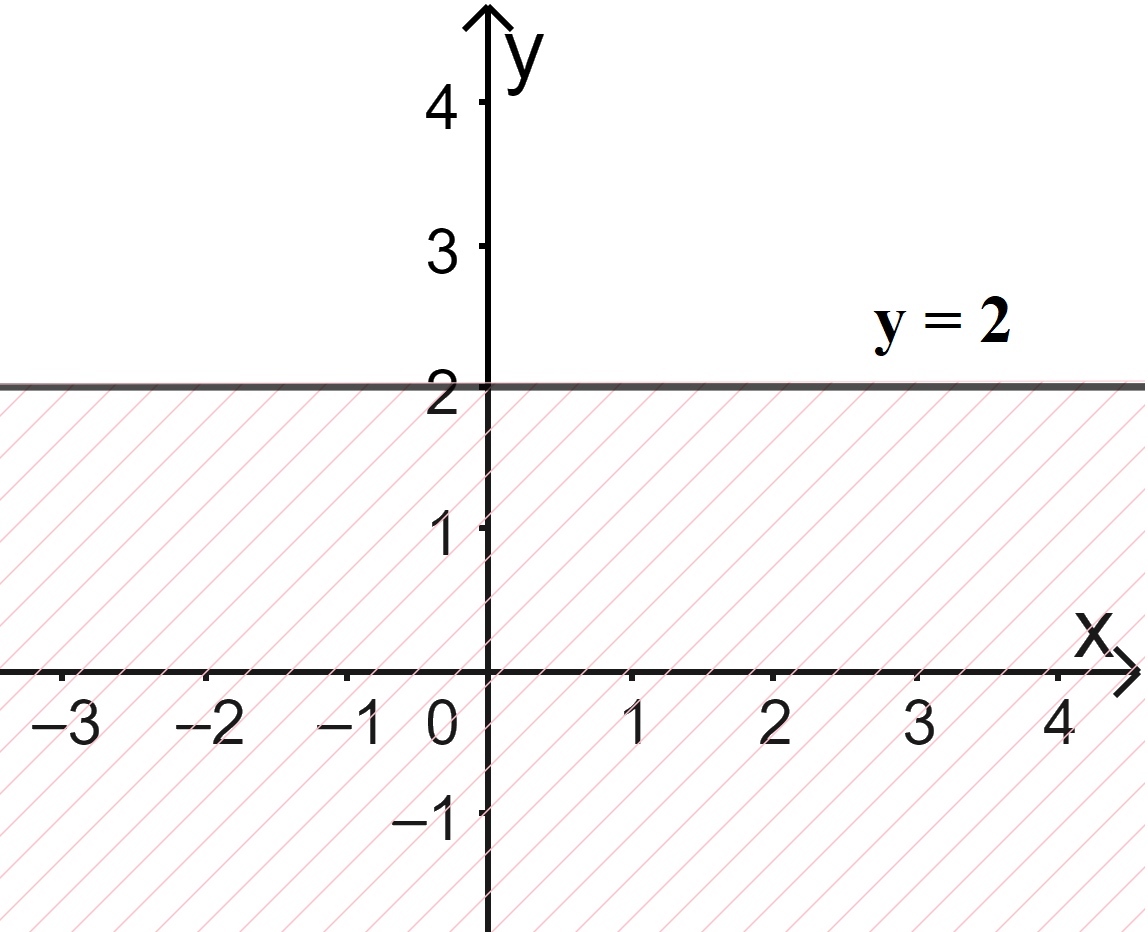
a) Vẽ đường thẳng \(\Delta :y = 2\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \({y_O} = 0 < 2\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
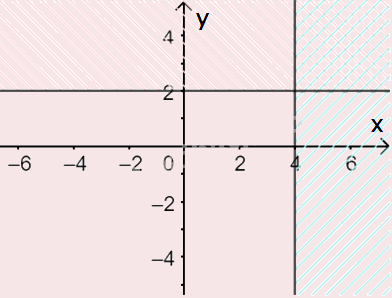
b) Vẽ đường thẳng \(\Delta ':x = 4\) đi qua hai điểm \(A'(4;0)\) và \(B'\left( {4;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta '\) và \({x_O} = 0 < 4\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Cho bất phương trình \(2x - y + 1 < 0\)
a) Vẽ đường thẳng \(y = 2x + 1\)
b) Các cặp số \(( - 2;0),(0;0),(1;1)\) có là nghiệm của bất phương trình đã cho không?
Lời giải chi tiết:
a) Đường thẳng \(y = 2x + 1\) đi qua điểm \(A(0;1)\) và \(B\left( { - \frac{1}{2};0} \right)\)
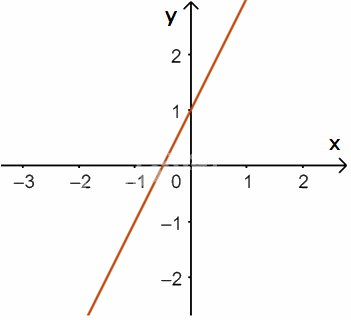
b)
Vì \(2.( - 2) - 0 + 1 = - 3 < 0\)nên \(( - 2;0)\) là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.0 - 0 + 1 = 1 > 0\)nên \((0;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.1 - 1 + 1 = 2 > 0\)nên \(( - 2;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Biểu diễn miền nghiệm của các bất phương trình sau:
a) \(2x + y - 2 \le 0\)
b) \(x - y - 2 \ge 0\)
Lời giải chi tiết:
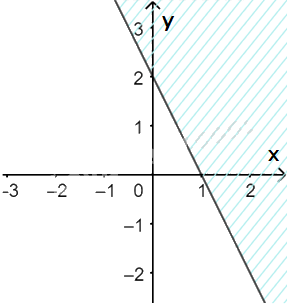
a) Vẽ đường thẳng \(\Delta :2x + y - 2 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 + 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
b) Vẽ đường thẳng \(\Delta :x - y - 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {2;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
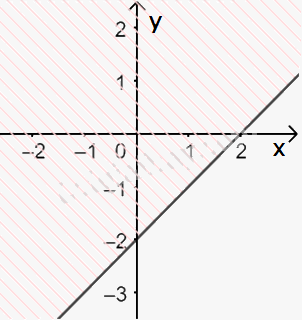
Biểu diễn miền nghiệm của hai bất phương trình sau trên cùng một mặt phẳng tọa độ Oxy:
a) \(y \ge 2\)
b) \(x \le 4\)
Lời giải chi tiết:
a) Vẽ đường thẳng \(\Delta :y = 2\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \({y_O} = 0 < 2\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
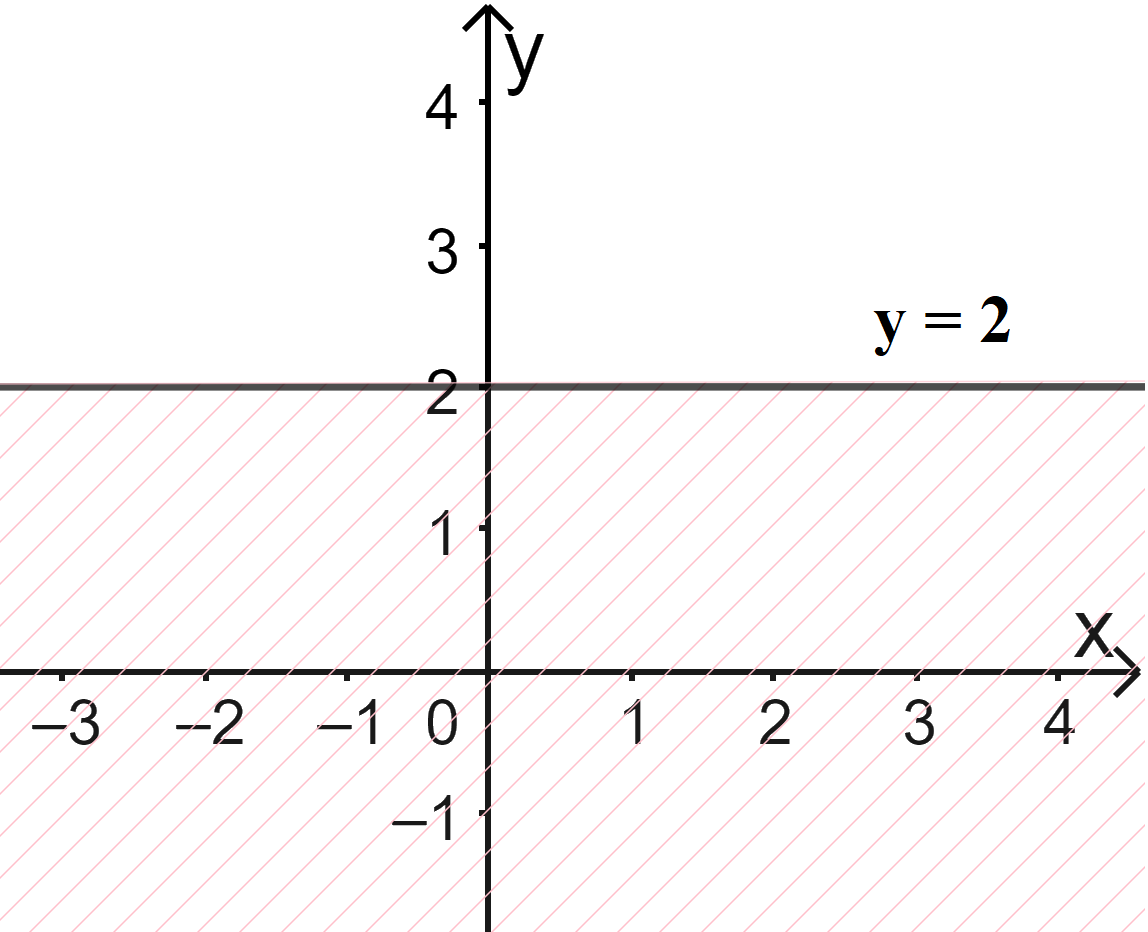
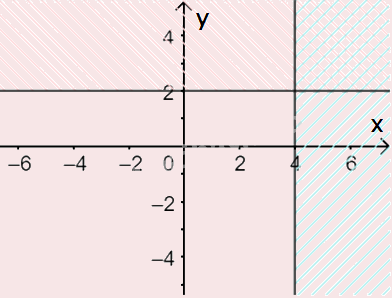
b) Vẽ đường thẳng \(\Delta ':x = 4\) đi qua hai điểm \(A'(4;0)\) và \(B'\left( {4;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta '\) và \({x_O} = 0 < 4\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Cho bất phương trình \(2x - y + 1 < 0\)
a) Vẽ đường thẳng \(y = 2x + 1\)
b) Các cặp số \(( - 2;0),(0;0),(1;1)\) có là nghiệm của bất phương trình đã cho không?
Lời giải chi tiết:
a) Đường thẳng \(y = 2x + 1\) đi qua điểm \(A(0;1)\) và \(B\left( { - \frac{1}{2};0} \right)\)
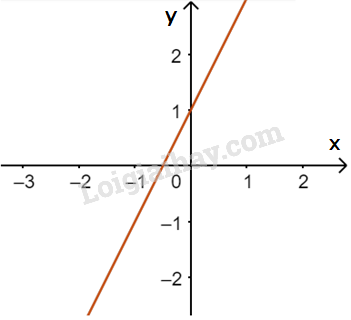
b)
Vì \(2.( - 2) - 0 + 1 = - 3 < 0\)nên \(( - 2;0)\) là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.0 - 0 + 1 = 1 > 0\)nên \((0;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.1 - 1 + 1 = 2 > 0\)nên \(( - 2;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Biểu diễn miền nghiệm của các bất phương trình sau:
a) \(2x + y - 2 \le 0\)
b) \(x - y - 2 \ge 0\)
Lời giải chi tiết:
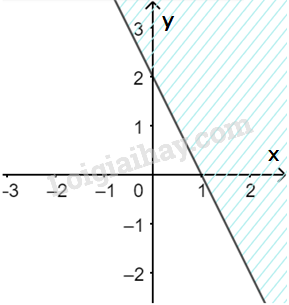
a) Vẽ đường thẳng \(\Delta :2x + y - 2 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 + 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
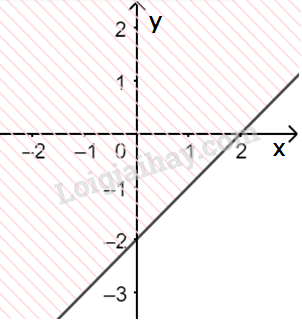
b) Vẽ đường thẳng \(\Delta :x - y - 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {2;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về vectơ, đặc biệt là các phép toán trên vectơ và ứng dụng của vectơ trong hình học. Việc nắm vững các khái niệm và kỹ năng trong mục này là nền tảng quan trọng cho việc học tập các kiến thức toán học ở các lớp trên.
Bài tập này yêu cầu học sinh thực hiện các phép cộng và trừ vectơ dựa trên các quy tắc đã học. Để giải các bài tập này, học sinh cần hiểu rõ khái niệm về vectơ, tọa độ của vectơ và quy tắc cộng, trừ vectơ.
Bài tập này yêu cầu học sinh thực hiện phép nhân vectơ với một số thực. Để giải các bài tập này, học sinh cần hiểu rõ quy tắc nhân vectơ với một số thực và ảnh hưởng của phép nhân này đến độ dài và hướng của vectơ.
Bài tập này yêu cầu học sinh sử dụng kiến thức về vectơ để giải các bài toán hình học, chẳng hạn như chứng minh hai đường thẳng song song, tìm tọa độ trung điểm của đoạn thẳng, hoặc tính diện tích của hình bình hành.
| Bài tập | Lời giải |
|---|---|
| Cho A(1; 2), B(3; 4). Tìm tọa độ trung điểm I của đoạn thẳng AB. | I = ((1+3)/2; (2+4)/2) = (2; 3) |
Để học tốt môn Toán 10, các em cần thường xuyên luyện tập, làm bài tập và tìm hiểu các kiến thức mới. Ngoài ra, các em cũng nên tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn học sinh khác.
Hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 3 trang 30, 31, 32 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!