Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 88, 89, 90 sách giáo khoa Toán 10 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: Cho hình thang ABCD có đáy là AB và CD. Cho biết
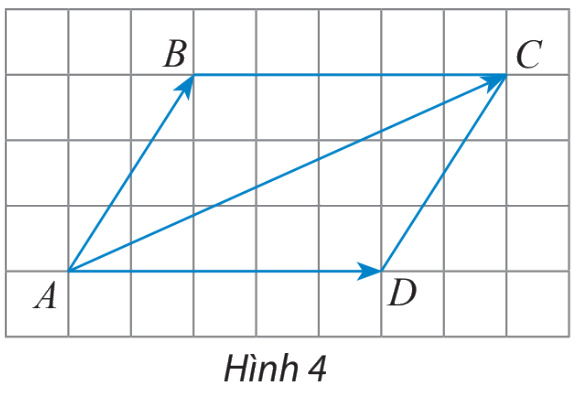
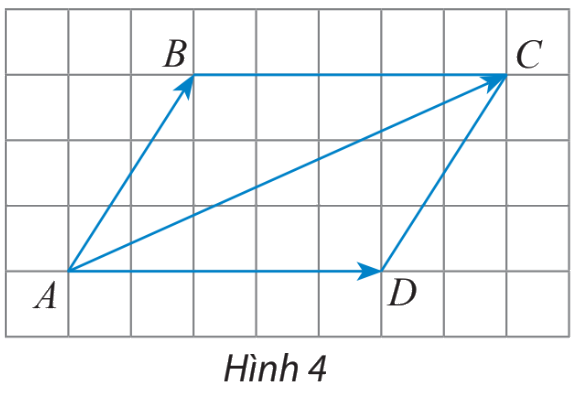
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Phương pháp giải:
Tìm vectơ bằng với vectơ \(\overrightarrow {AD} \), sau đó áp dụng quy tắc ba điểm
Lời giải chi tiết:
Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)(đpcm)
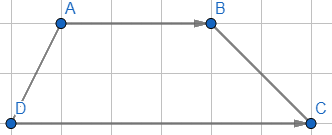
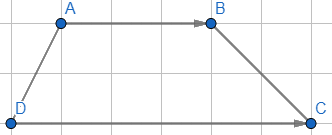
Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} ;\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Phương pháp giải:
Bước 1: Áp dụng quy tắc ba điểm, tìm vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
Bước 2: Xác định hướng của vectơ vừa tìm được
Bước 3: So sánh hướng của 2 vectơ
Lời giải chi tiết:
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
Phương pháp giải:
Bước 1: Dựng hình bình hành ABDC
Bước 2: Áp dụng quy tắc hình bình hành tìm tổng vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \)
Bước 3: Tìm độ dài vectơ tổng.
Lời giải chi tiết:
Dựng hình bình hành ABDC.
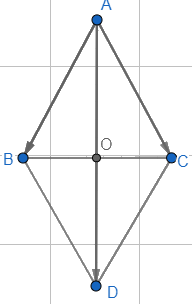
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
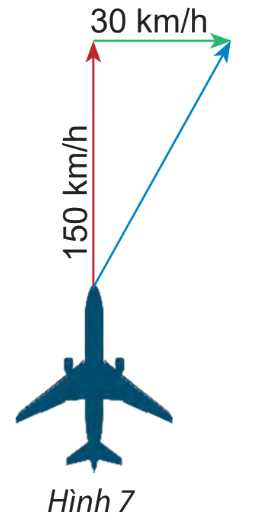
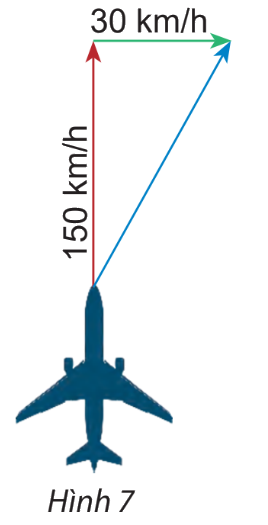
Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.
Phương pháp giải:
Bước 1: Áp dụng quy tắc 3 điểm để tìm vectơ tổng
Bước 2: Tìm độ dài vectơ tổng vừa tìm được.
Lời giải chi tiết:
Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
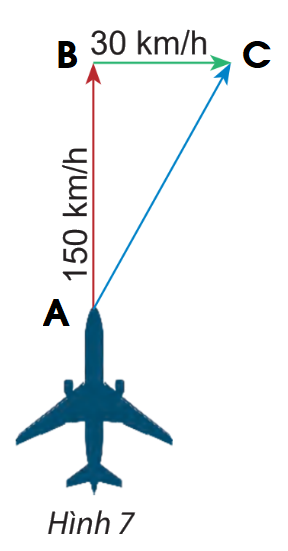
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h
Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên.
Phương pháp giải:
Xác định A là điểm đầu và C là điểm cuối, dùng đoạn thẳng có hướng nối 2 điểm trên.
Lời giải chi tiết:
Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.
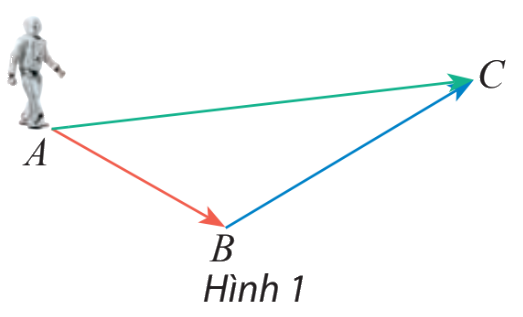
Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)
Lời giải chi tiết:
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
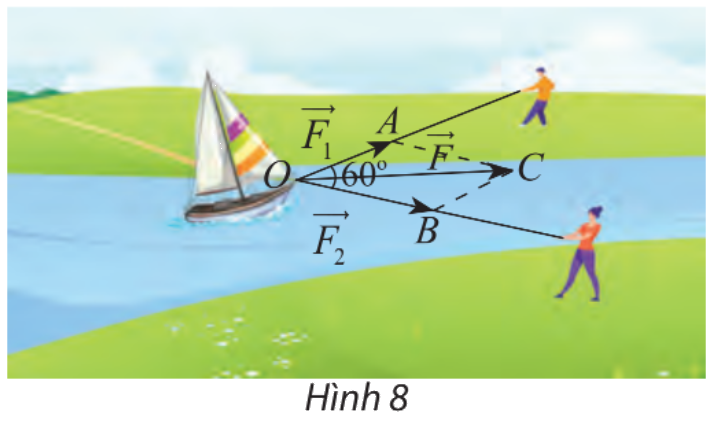
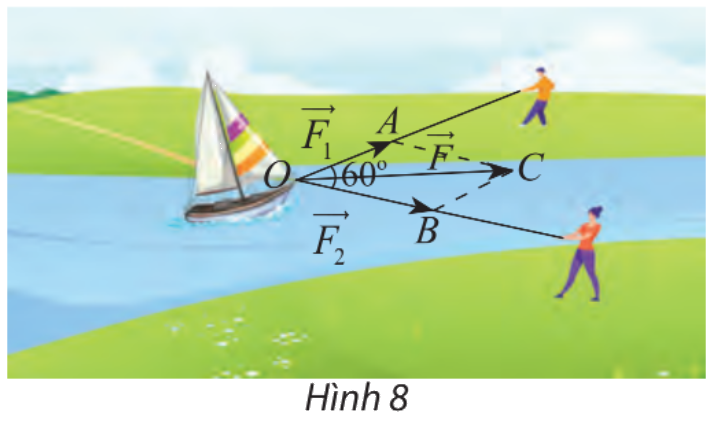
Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)
Phương pháp giải:
Bước 1: Dựng hình bình hành AOBC
Bước 2: Áp dụng quy tắc hình bình hành tìm tổng lực
Bước 3: Xác định độ lớn của vectơ tổng.
Lời giải chi tiết:
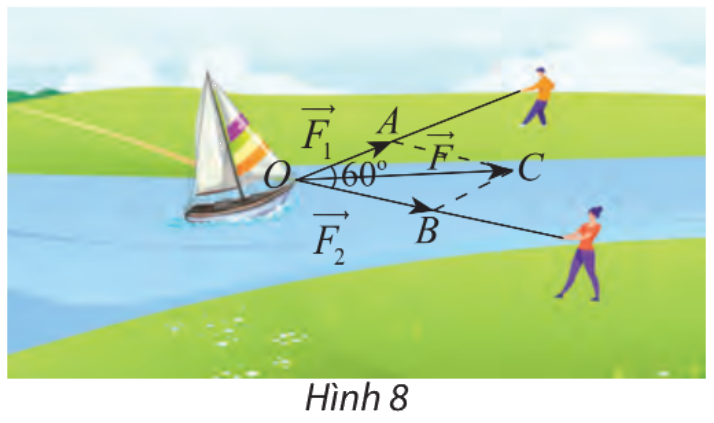
Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \);
\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).
Áp dụng định lý cos ta có:
\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)
\( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )} \simeq 871,78\)N
Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N
Lời giải chi tiết:
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên.
Phương pháp giải:
Xác định A là điểm đầu và C là điểm cuối, dùng đoạn thẳng có hướng nối 2 điểm trên.
Lời giải chi tiết:
Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.
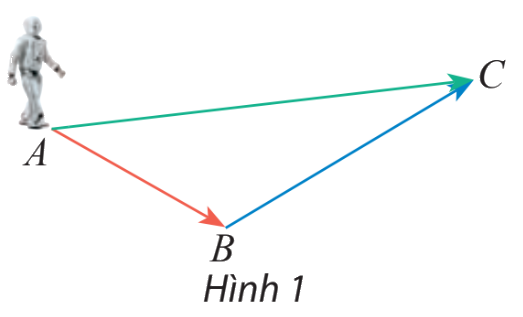
Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ \(\overrightarrow {AC} \)
Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Phương pháp giải:
Tìm vectơ bằng với vectơ \(\overrightarrow {AD} \), sau đó áp dụng quy tắc ba điểm
Lời giải chi tiết:
Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)(đpcm)
Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} ;\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Phương pháp giải:
Bước 1: Áp dụng quy tắc ba điểm, tìm vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
Bước 2: Xác định hướng của vectơ vừa tìm được
Bước 3: So sánh hướng của 2 vectơ
Lời giải chi tiết:
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
Phương pháp giải:
Bước 1: Dựng hình bình hành ABDC
Bước 2: Áp dụng quy tắc hình bình hành tìm tổng vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \)
Bước 3: Tìm độ dài vectơ tổng.
Lời giải chi tiết:
Dựng hình bình hành ABDC.
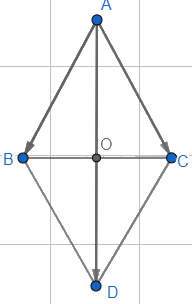
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} - B{O^2}} = \sqrt {A{B^2} - {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)
Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.
Phương pháp giải:
Bước 1: Áp dụng quy tắc 3 điểm để tìm vectơ tổng
Bước 2: Tìm độ dài vectơ tổng vừa tìm được.
Lời giải chi tiết:
Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
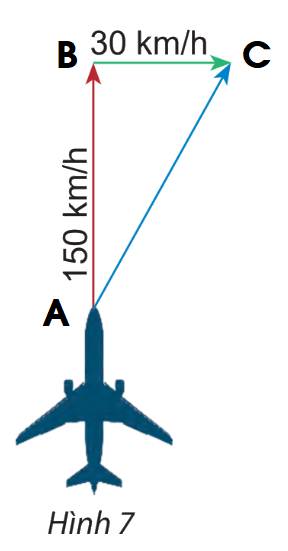
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h
Hai người cùng kéo một con thuyền với hai lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} \) có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là \({60^\circ }\). Tìm độ lớn của vectơ hợp lực \(\overrightarrow F \) là tổng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)
Phương pháp giải:
Bước 1: Dựng hình bình hành AOBC
Bước 2: Áp dụng quy tắc hình bình hành tìm tổng lực
Bước 3: Xác định độ lớn của vectơ tổng.
Lời giải chi tiết:
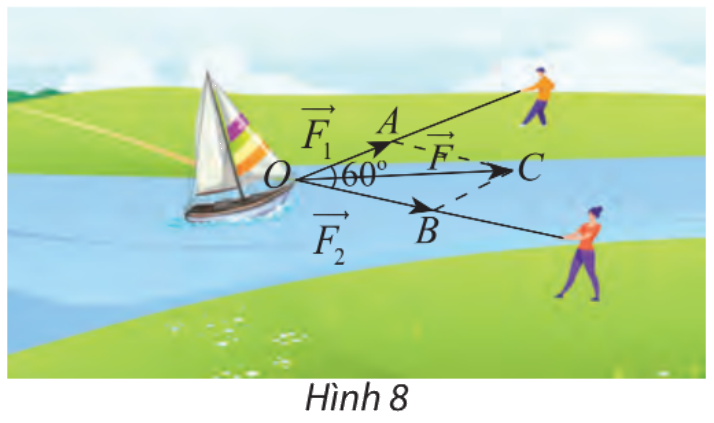
Áp dụng quy tắc hình bình hành ta có: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \);
\(AC = OB = 600\); \(\widehat {AOB} = 60^\circ \Rightarrow \widehat {OAC} = 120^\circ \) (hai góc bù nhau trong hình bình hành).
Áp dụng định lý cos ta có:
\(OC = \sqrt {O{A^2} + A{C^2} - 2OA.AC.\cos (120^\circ )} \)
\( = \sqrt {{{400}^2} + {{600}^2} - 2.400.600.\cos (120^\circ )} \simeq 871,78\)N
Vậy độ lớn của vectơ hợp lực \(\overrightarrow F \) gần bằng 871,78 N
Mục 1 của chương trình Toán 10 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về tập hợp, các phép toán trên tập hợp, và các khái niệm cơ bản về số thực. Việc nắm vững những kiến thức này là nền tảng quan trọng cho việc học tập các chương tiếp theo.
Bài tập này yêu cầu học sinh vận dụng các kiến thức về tập hợp, bao gồm:
Lời giải chi tiết sẽ hướng dẫn các em từng bước thực hiện các phép toán, đồng thời giải thích rõ ràng ý nghĩa của từng kết quả.
Bài tập này tập trung vào việc ôn tập các khái niệm về số thực, bao gồm:
Chúng tôi sẽ cung cấp các ví dụ minh họa cụ thể để giúp các em hiểu rõ hơn về các khái niệm này.
Bài tập này yêu cầu học sinh vận dụng kiến thức về giá trị tuyệt đối của một số thực để giải các bài toán liên quan đến:
Lời giải sẽ trình bày các bước giải một cách rõ ràng, logic và dễ hiểu.
Để giải các bài tập trong mục 1 này một cách hiệu quả, các em cần:
Ví dụ 1: Cho A = {1, 2, 3} và B = {2, 4, 5}. Tìm A ∪ B và A ∩ B.
Lời giải:
Ví dụ 2: Tính giá trị tuyệt đối của -3.5.
Lời giải:
|-3.5| = 3.5
Khi giải các bài tập về tập hợp, các em cần chú ý đến thứ tự của các phần tử trong tập hợp. Khi giải các bài tập về số thực, các em cần chú ý đến các quy tắc về dấu và thứ tự thực hiện các phép toán.
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc học tập môn Toán 10 tập 1 - Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất!
| Bài tập | Trang | Độ khó |
|---|---|---|
| Bài 1 | 88 | Dễ |
| Bài 2 | 89 | Trung bình |
| Bài 3 | 90 | Trung bình |