Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 63, 64 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
Tính
Tìm góc \(\alpha ({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:
a) \(\sin \alpha = \frac{{\sqrt 3 }}{2}\)
b) \(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\)
c) \(\tan \alpha = - 1\)
d) \(\cot \alpha = - \sqrt 3 \)
Phương pháp giải:
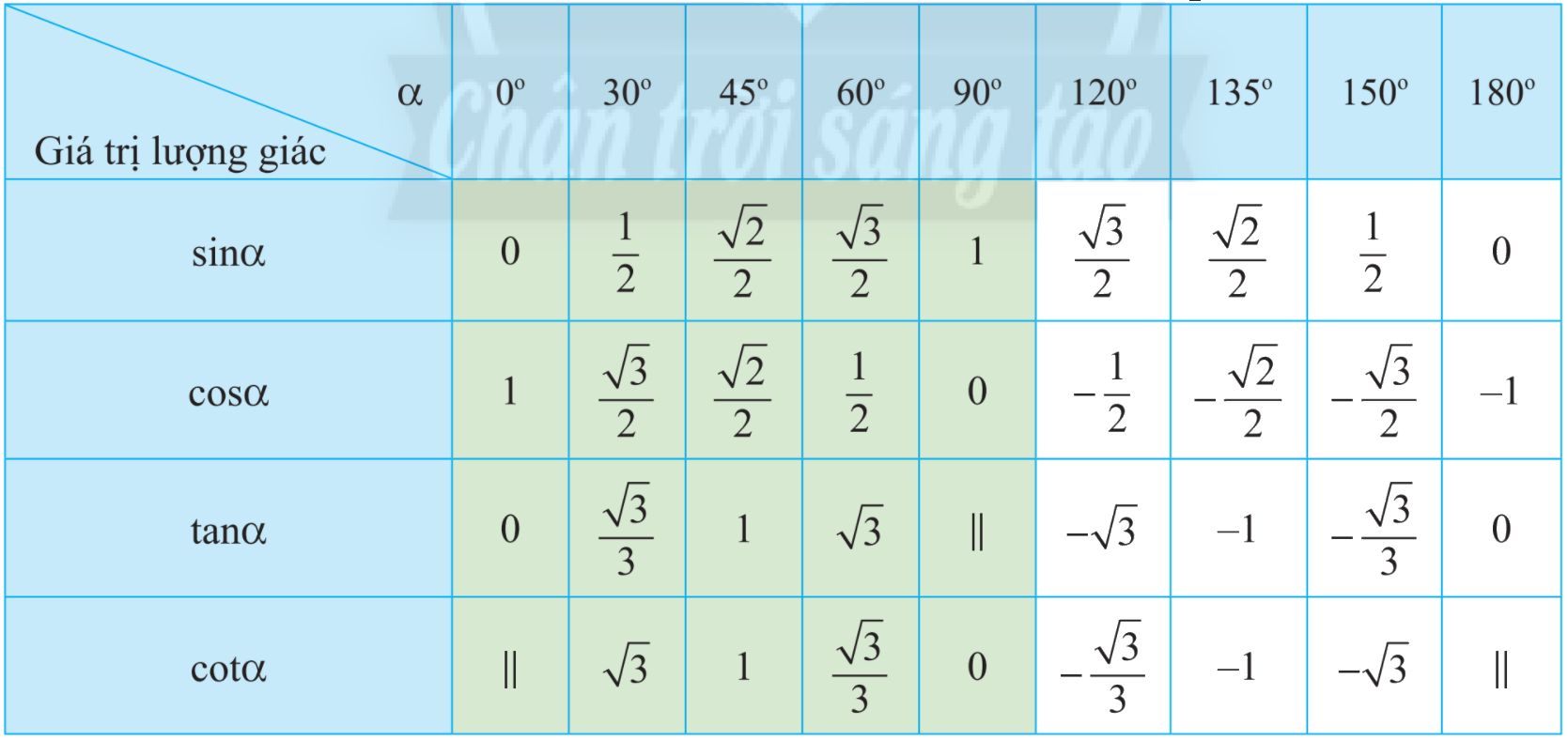
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.
Lời giải chi tiết:
a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = \frac{{\sqrt 3 }}{2}\) với \(\alpha = {60^o}\) và \(\alpha = {120^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = - 1\) với \(\alpha = {135^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha = - \sqrt 3 \) với \(\alpha = {150^o}\)
Tính:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
Phương pháp giải:
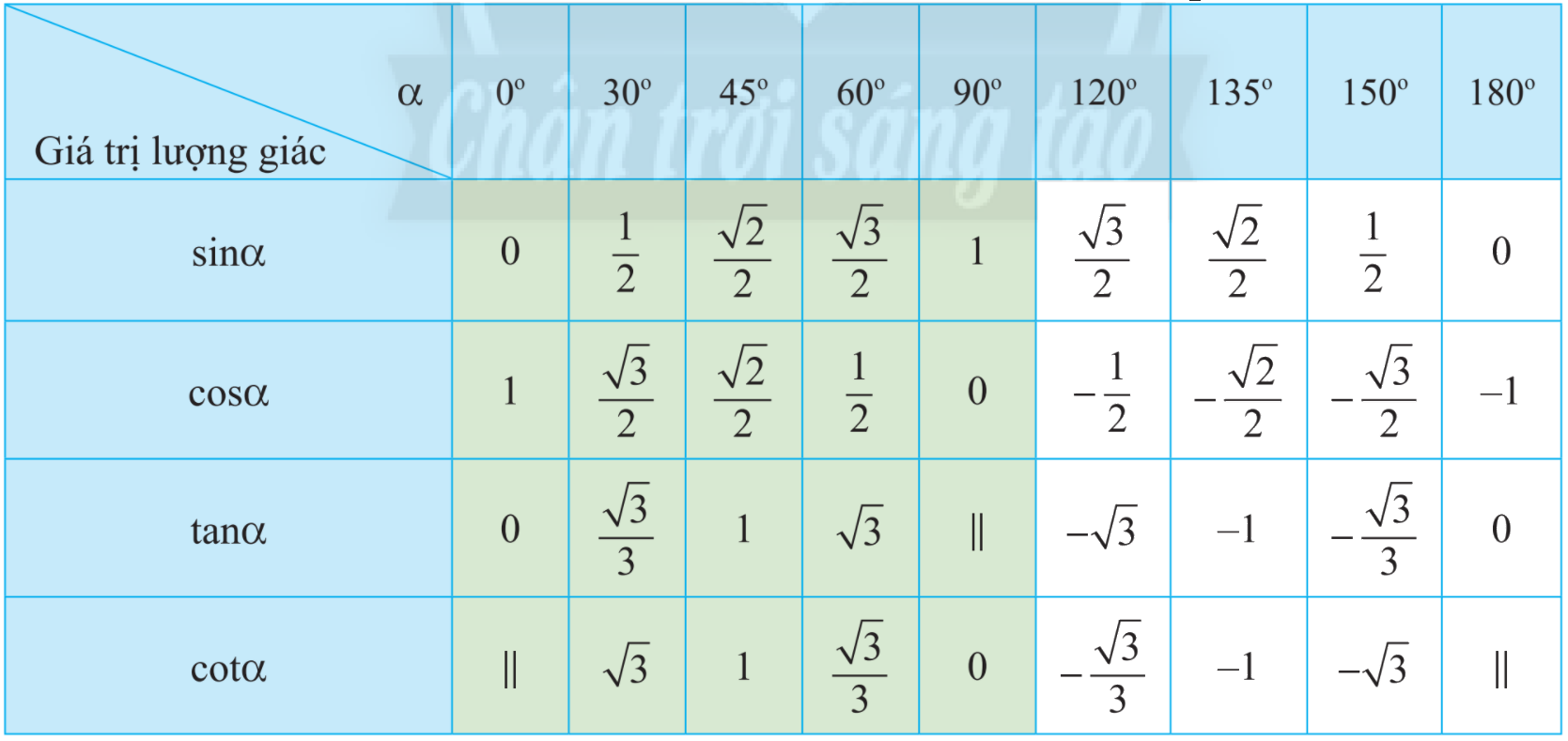
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.
Lời giải chi tiết:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\tan {135^o} = - 1;\cot {45^o} = 1.\)
\( \Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = - \frac{{\sqrt 3 }}{3};\cot {135^o} = - 1.\)
\( \Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 2\sqrt 3 + 1.\)
Tìm góc \(\alpha ({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:
a) \(\sin \alpha = \frac{{\sqrt 3 }}{2}\)
b) \(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\)
c) \(\tan \alpha = - 1\)
d) \(\cot \alpha = - \sqrt 3 \)
Phương pháp giải:
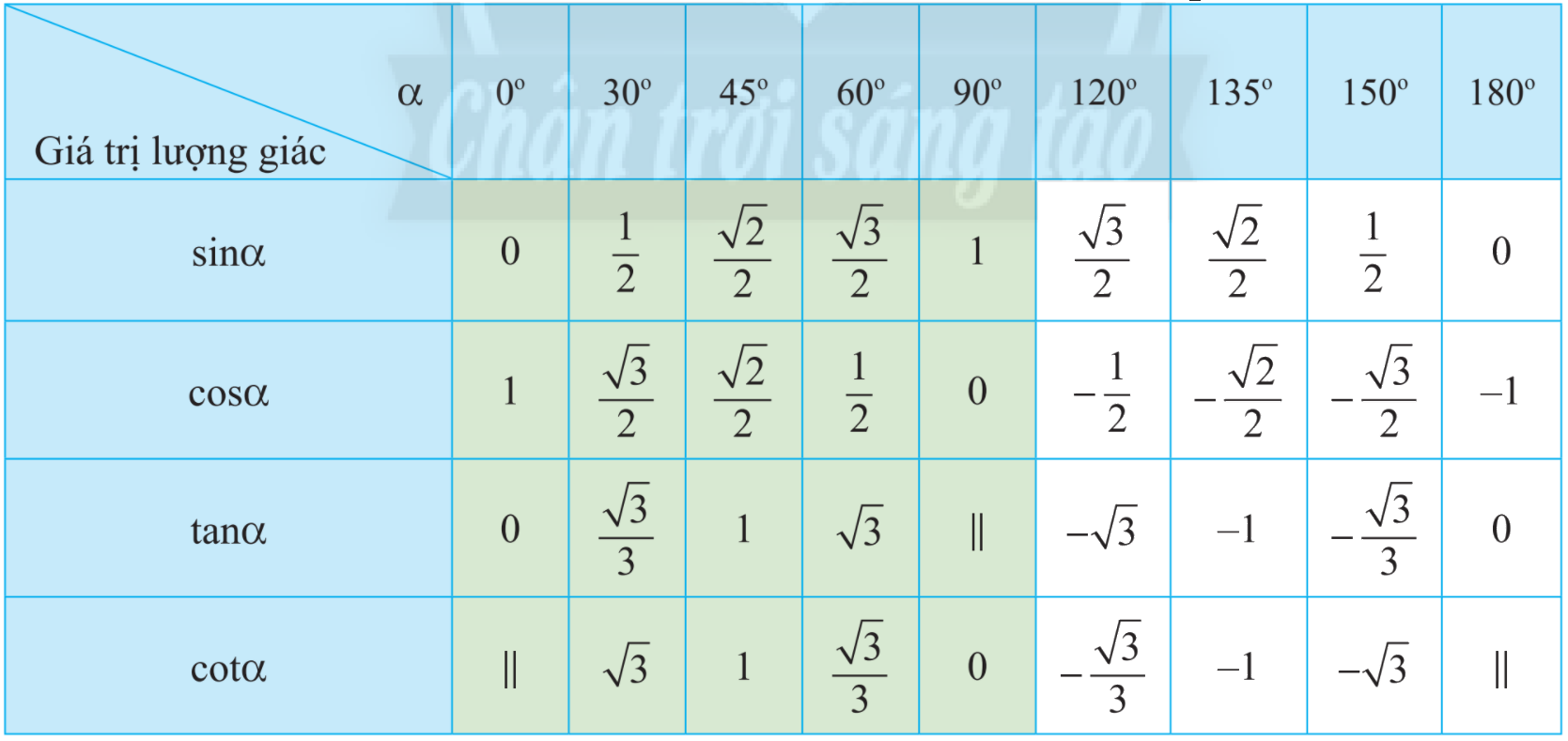
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.
Lời giải chi tiết:
a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = \frac{{\sqrt 3 }}{2}\) với \(\alpha = {60^o}\) và \(\alpha = {120^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = - 1\) với \(\alpha = {135^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha = - \sqrt 3 \) với \(\alpha = {150^o}\)
Tính:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
Phương pháp giải:
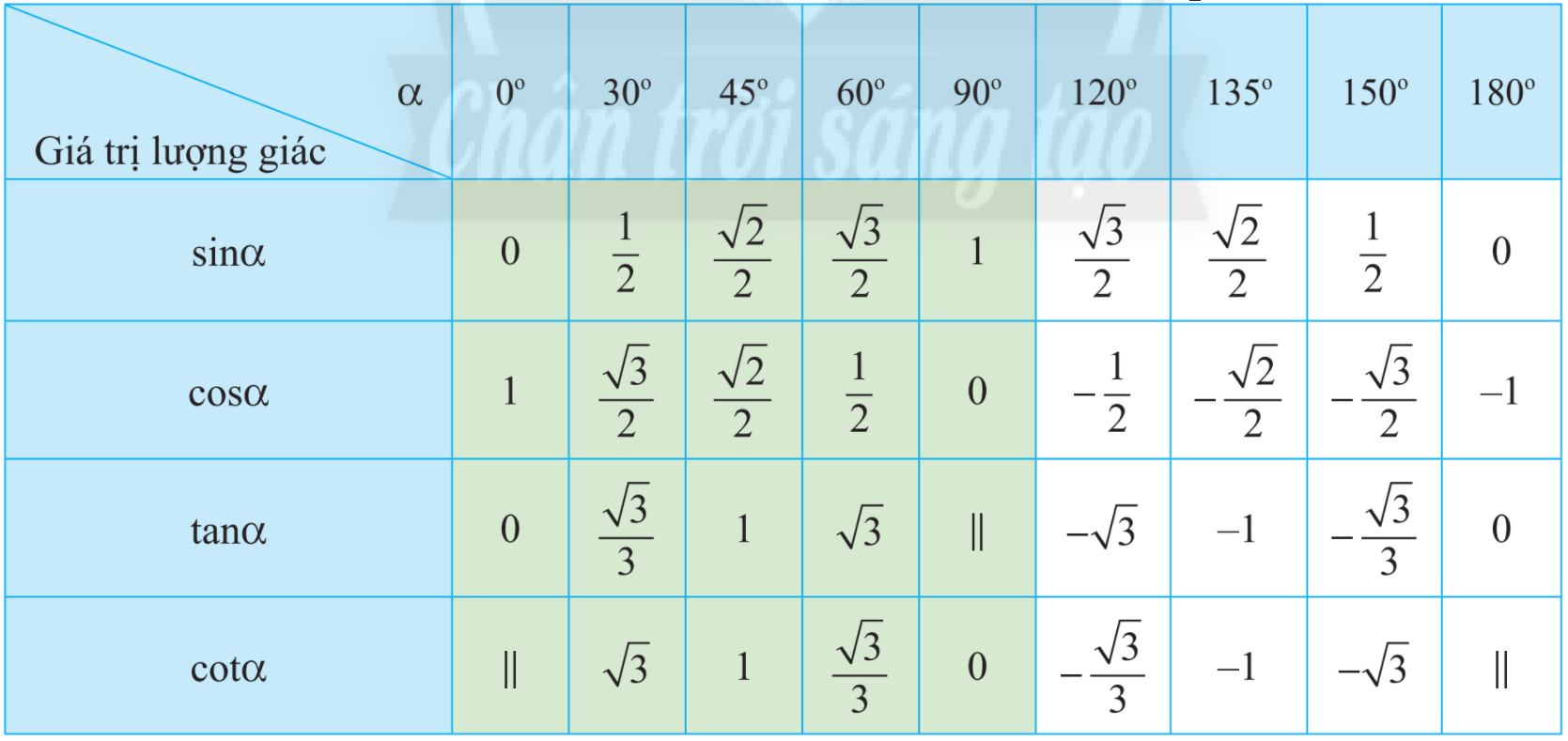
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt.
Lời giải chi tiết:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\tan {135^o} = - 1;\cot {45^o} = 1.\)
\( \Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = - \frac{{\sqrt 3 }}{3};\cot {135^o} = - 1.\)
\( \Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 2\sqrt 3 + 1.\)
Mục 3 trong SGK Toán 10 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học. Cụ thể, các bài tập trong mục này thường liên quan đến việc xác định tọa độ của vectơ, thực hiện các phép toán vectơ (cộng, trừ, nhân với một số thực) và sử dụng vectơ để chứng minh các tính chất hình học.
Bài tập mục 3 trang 63, 64 SGK Toán 10 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập sau:
Để tìm tọa độ của vectơ AB, ta sử dụng công thức: AB = (xB - xA; yB - yA), trong đó A(xA; yA) và B(xB; yB).
Ví dụ: Cho A(1; 2) và B(3; 4). Khi đó, AB = (3 - 1; 4 - 2) = (2; 2).
Cho hai vectơ a = (x1; y1) và b = (x2; y2). Khi đó:
Ví dụ: Cho a = (1; 2) và b = (3; 4). Khi đó, a + b = (1 + 3; 2 + 4) = (4; 6) và a - b = (1 - 3; 2 - 4) = (-2; -2).
Cho vectơ a = (x; y) và một số thực k. Khi đó, ka = (kx; ky).
Ví dụ: Cho a = (1; 2) và k = 3. Khi đó, 3a = (3 * 1; 3 * 2) = (3; 6).
Kiến thức về vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập mục 3 trang 63, 64 SGK Toán 10 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!