Chào mừng bạn đến với bài học về Lý thuyết Tọa độ của vecto, một phần quan trọng trong chương trình Toán 10 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về tọa độ của vecto, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học tập trực tuyến tốt nhất với nội dung được trình bày rõ ràng, dễ hiểu và có nhiều bài tập thực hành để bạn củng cố kiến thức.
A. Lý thuyết 1. Tọa độ của vecto đối với một hệ trục tọa độ a) Trục tọa độ Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đồ thị xác định một điểm O (gọi là điểm gốc) và một vectơ e có độ dài bằng 1 gọi là vectơ đơn vị của trục.
A. Lý thuyết
1. Tọa độ của vecto đối với một hệ trục tọa độ
a) Trục tọa độ
Trục tọa độ (gọi tắt là trục) là một đường thẳng trên đồ thị xác định một điểm O (gọi là điểm gốc) và một vectơ e có độ dài bằng 1 gọi là vectơ đơn vị của trục.
Ta ký hiệu trục đó là (O;e).

b) Hệ trục tọa độ
Hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) gồm hai trục \(\left( {O;\overrightarrow i } \right)\) và \(\left( {O;\overrightarrow j } \right)\) vuông góc với nhau. Điểm góc O chung của hai trục gọi là gốc tọa độ.
Trục \(\left( {O;\overrightarrow i } \right)\) được gọi là trục hoành và ký hiệu là Ox, trục \(\left( {O;\overrightarrow j } \right)\) được gọi là trục tung và ký hiệu là Oy. Các vectơ \(\overrightarrow i \) và \(\overrightarrow j \) là các vectơ đơn vị trên Ox và Oy. Hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) còn được ký hiệu là Oxy.
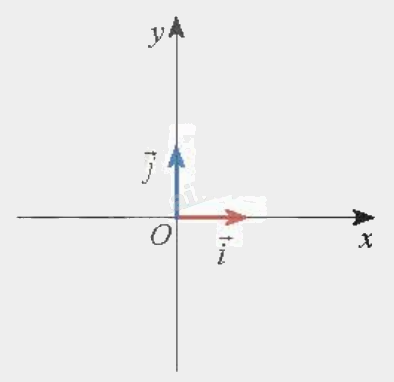
c) Tọa độ của một vecto
| Trong mặt phẳng Oxy, cặp số (x;y) trong biểu diễn \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j \) được gọi là tọa độ của vecto \(\overrightarrow a \), kí hiệu \(\overrightarrow a = (x;y)\), x gọi là hoành độ, y gọi là tung độ của vecto \(\overrightarrow a \). |
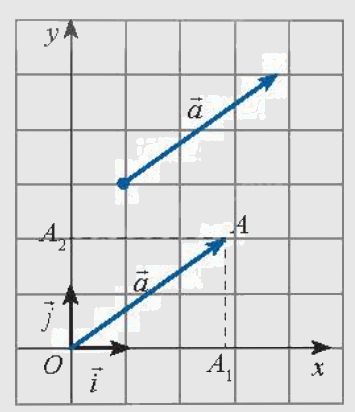
Chú ý:
+ \(\overrightarrow a = (x;y) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j \).
+ Nếu \(\overrightarrow a = ({x_1};{y_1})\) và \(\overrightarrow b = ({x_2};{y_2})\) thì \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\).
d) Tọa độ của một điểm
| Trong mặt phẳng tọa độ, cho điểm M tùy ý. Tọa độ của vecto \(\overrightarrow {OM} \) được gọi là tọa độ của điểm M. |
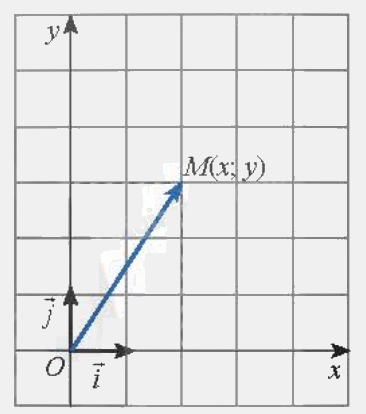
Chú ý: Trong mặt phẳng tọa độ Oxy, ta có:
+ \(M(x;y) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j \).
+ Nếu \(\overrightarrow {OM} = (x;y)\) thì x gọi là hoành độ, y gọi là tung độ của điểm M.
2. Biểu thức tọa độ của các phép toán vecto
Cho hai vecto \(\overrightarrow a = ({a_1};{a_2})\), \(\overrightarrow b = ({b_1};{b_2})\) và số thực k. Khi đó: + \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2})\). + \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2})\). + \(k\overrightarrow a = (k{a_1};k{a_2})\) với \(k \in \mathbb{R}\). + \(\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2}\). |
3. Áp dụng của tọa độ vecto
a) Liên hệ giữa tọa độ của điểm và tọa độ của vecto trong mặt phẳng
Cho hai điểm \(A({x_A};{y_A})\), \(B({x_B};{y_B})\). Ta có: \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\). |
b) Tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác
Cho hai điểm \(A({x_A};{y_A})\) và \(B({x_B};{y_B})\). Nếu \(M({x_M};{y_M})\) là trung điểm đoạn thẳng AB thì \({x_M} = \frac{{{x_A} + {x_B}}}{2}\); \({y_M} = \frac{{{y_A} + {y_B}}}{2}\). Cho tam giác ABC có \(A({x_A};{y_A})\), \(B({x_B};{y_B})\), \(C({x_C};{y_C})\). Nếu \(G({x_G};{y_G})\) là trọng tâm tam giác ABC thì \({x_M} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\); \({y_M} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\). |
c) Ứng dụng biểu thức tọa độ của các phép toán vecto
Cho hai vecto \(\overrightarrow a = ({a_1};{a_2})\), \(\overrightarrow b = ({b_1};{b_2})\) và hai điểm \(A({x_A};{y_A})\) và \(B({x_B};{y_B})\). Ta có: + \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow {a_1}{b_1} + {a_2}{b_2} = 0\). + \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương \( \Leftrightarrow {a_1}{b_2} - {a_2}{b_1} = 0\). + \(\left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {a_2}^2} \). + \(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \). + \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {{a_1}^2 + {a_2}^2} .\sqrt {{b_1}^2 + {b_2}^2} }}\) (\(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \)). |
B. Bài tập
Bài 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M, N, P, Q. Tìm tọa độ các vecto \(\overrightarrow {OM} \), \(\overrightarrow {ON} \), \(\overrightarrow {OP} \), \(\overrightarrow {OQ} \).
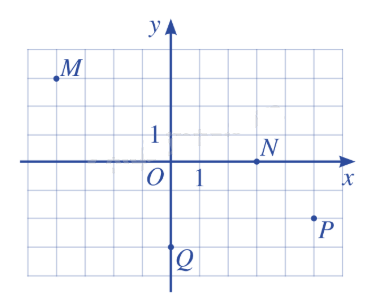
Giải:
Từ hình vẽ, ta có: M(-4;3), N(3;0), P(5;-2), Q(0;-3).
Do đó: \(\overrightarrow {OM} = ( - 4;3)\), \(\overrightarrow {ON} = (3;0)\), \(\overrightarrow {OP} = (5; - 2)\), \(\overrightarrow {OQ} = (0; - 3)\).
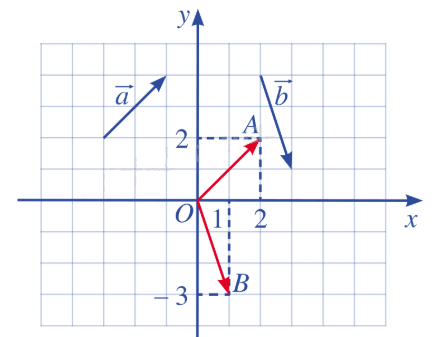
Bài 2: Tìm tọa độ của các vecto \(\overrightarrow a \), \(\overrightarrow b \) trong hình.
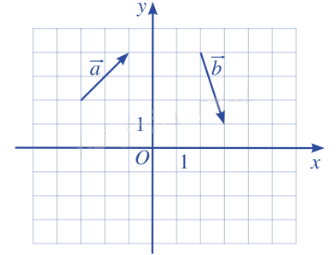
Giải:
Ta có:
\(\overrightarrow a = \overrightarrow {OA} \) và A(2;2); tọa độ vecto \(\overrightarrow {OA} \) chính là tọa độ điểm A nên \(\overrightarrow a = (2;2)\).
\(\overrightarrow b = \overrightarrow {OB} \) và A(1;-3); tọa độ vecto \(\overrightarrow {OB} \) chính là tọa độ điểm B nên \(\overrightarrow b = (1; - 3)\).
Bài 3: Trong mặt phẳng tọa độ Oxy, cho điểm A(1;2) và vecto \(\overrightarrow u = (3; - 4)\).
a) Biểu diễn vecto \(\overrightarrow u \) qua hai vecto \(\overrightarrow i \) và \(\overrightarrow j \).
b) Biểu diễn vecto \(\overrightarrow {OA} \) qua hai vecto \(\overrightarrow i \) và \(\overrightarrow j \).
Giải:
a) Vì \(\overrightarrow u = (3; - 4)\) nên \(\overrightarrow u = 3\overrightarrow i + ( - 4)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j \).
b) Vì điểm A có tọa độ là (1;2) nên \(\overrightarrow {OA} = (1;2)\). Do đó:
\(\overrightarrow {OA} = 1\overrightarrow i + 2\overrightarrow j = \overrightarrow i + 2\overrightarrow j \).
Bài 4: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(1;1), B(4;3), C(-1;-2).
a) Tìm tọa độ của vecto \(\overrightarrow {AB} \).
b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.
Giải:
a) Ta có: \(\overrightarrow {AB} = (4 - 1;3 - 1)\). Vậy \(\overrightarrow {AB} = (3;2)\).
b) Gọi tọa độ của điểm D là \(({x_D};{y_D})\), ta có: \(\overrightarrow {DC} = ( - 1 - {x_D}; - 2 - {y_D})\).
Tứ giác ABCD là hình bình hành khi và chỉ khi:
\(\overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {DC} = (3;2) \Leftrightarrow \left\{ \begin{array}{l} - 1 - {x_D} = 3\\ - 2 - {y_D} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = - 4\\{y_D} = - 4\end{array} \right.\).
Vậy D(-4;-4).
Bài 5: Cho \(\overrightarrow u = (2; - 1)\), \(\overrightarrow v = (1;5)\). Tìm tọa độ của \(\overrightarrow u + \overrightarrow v \) và \(\overrightarrow u - \overrightarrow v \).
Giải:
\(\overrightarrow u + \overrightarrow v = (2 + 1; - 1 + 5) = (3;4)\); \(\overrightarrow u - \overrightarrow v = (2 - 1; - 1 - 5) = (1; - 6)\).
Bài 6: Cho ba điểm A(-1;-3), B(2;3) và C(3;5). Chứng minh ba điểm A, B, C thẳng hàng.
Giải:
Ta có: \(\overrightarrow {AB} = (3;6)\), \(\overrightarrow {BC} = (1;2)\). Suy ra \(\overrightarrow {AB} = 3\overrightarrow {BC} \).
Vậy ba điểm A, B, C thẳng hàng.
Bài 7: Cho tma giác ABC có A(-2;1), B(2;5), C(5;2). Tìm tọa độ trung điểm M của đoạn thẳng AB và trọng tâm G của tam giác ABC.
Giải:
Do \(M({x_M};{y_M})\) là trung điểm của đoạn thẳng AB nên:
\({x_M} = \frac{{ - 2 + 2}}{2} = 0\); \({y_M} = \frac{{1 + 5}}{2} = 3\).
Vậy M(0;3).
Do \(G({x_G};{y_G})\) là trọng tâm tam giác ABC nên:
\({x_G} = \frac{{ - 2 + 2 + 5}}{3} = \frac{5}{3}\); \({y_G} = \frac{{1 + 5 + 2}}{3} = \frac{8}{3}\).
Vậy \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\).
Bài 8: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;2), B(1;-1), C(8;0).
a) Tính \(\overrightarrow {BA} .\overrightarrow {BC} \) và \(\cos \widehat {ABC}\).
b) Chứng minh \(\overrightarrow {AB} \bot \overrightarrow {AC} \).
c) Giải tam giác ABC.
Giải:
a) Ta có \(\overrightarrow {BA} = (1;3)\), \(\overrightarrow {BC} = (7;1)\). Do đó \(\overrightarrow {BA} .\overrightarrow {BC} = 1.7 + 3.1 = 10\).
Mặt khác: \(\left| {\overrightarrow {BA} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} \), \(\left| {\overrightarrow {BC} } \right| = \sqrt {{7^2} + {1^2}} = \sqrt {50} \).
\(\cos \widehat {ABC} = \cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{10}}{{\sqrt {10} .\sqrt {50} }} = \frac{{\sqrt 5 }}{5}\).
b) Do \(\overrightarrow {AB} = ( - 1; - 3)\) và \(\overrightarrow {AC} = (6; - 2)\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = ( - 1).6 + ( - 3).( - 2) = 0\).
Vậy \(\overrightarrow {AB} \bot \overrightarrow {AC} \).
c) Do \(\overrightarrow {AB} \bot \overrightarrow {AC} \) nên \(\widehat {BAC} = {90^o}\), tức tam giác ABC vuông tại A.
Mà \(\cos \widehat {ABC} = \frac{{\sqrt 5 }}{5}\) nên \(\widehat {ABC} \approx {63^o}\). Vì thế \(\widehat {ACB} \approx {90^o} - {63^o} = {27^o}\).
Mặt khác: \(AB = \left| {\overrightarrow {BA} } \right| = \sqrt {10} \), \(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {50} = 5\sqrt 2 \),
\(CA = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{\left( {5\sqrt 2 } \right)}^2} - {{\left( {\sqrt {10} } \right)}^2}} = 2\sqrt {10} \).
Trong chương trình Toán 10, phần tọa độ của vecto đóng vai trò then chốt trong việc xây dựng nền tảng cho các kiến thức hình học phân tích ở các lớp trên. Bài viết này sẽ trình bày chi tiết lý thuyết tọa độ của vecto theo SGK Toán 10 Chân trời sáng tạo, kèm theo các ví dụ minh họa và bài tập vận dụng để giúp học sinh hiểu sâu sắc và nắm vững kiến thức.
Trước khi đi vào tọa độ của vecto, chúng ta cần ôn lại một số khái niệm cơ bản về vectơ:
Hệ tọa độ Oxy là một hệ tọa độ vuông góc, bao gồm hai trục vuông góc nhau: trục hoành (Ox) và trục tung (Oy). Giao điểm của hai trục là gốc tọa độ O.
Tọa độ của một vectơ được biểu diễn bằng cặp số (x; y), trong đó x là hoành độ và y là tung độ của vectơ. Nếu A(xA; yA) và B(xB; yB) là hai điểm trong hệ tọa độ Oxy, thì vectơ AB có tọa độ là (xB - xA; yB - yA).
Khi thực hiện các phép toán vectơ trong hệ tọa độ, ta thực hiện các phép toán tương ứng trên các tọa độ của chúng:
Nếu M là điểm có tọa độ (xM; yM) và O là gốc tọa độ (0; 0), thì vectơ OM có tọa độ là (xM; yM).
Tọa độ vectơ có nhiều ứng dụng trong hình học và vật lý, ví dụ:
Dưới đây là một số bài tập vận dụng để giúp bạn củng cố kiến thức về tọa độ của vectơ:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Tọa độ của vecto - SGK Toán 10 Chân trời sáng tạo. Chúc bạn học tập tốt!