Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 10 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2 Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {{u_1};{u_2}} \right)\) là vectơ chỉ phương. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), tìm tọa độ của điểm M theo tọa độ của \({M_0}\) và \(\overrightarrow u \)
Phương pháp giải:
M và \({M_0}\) thuộc \(\Delta \) nên \({\overrightarrow {MM} _0}\) làm vectơ chỉ phương
Lời giải chi tiết:
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\) mà \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương nên ta có:
\(\left\{ \begin{array}{l}{x_0} - x = {u_1}\\{y_0} - y = {u_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - {u_1}\\y = {y_0} - {u_2}\end{array} \right.\)
Vậy \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
a) Viết phương trình tham số của đường thẳng d đi qua điểm \(B( - 9;5)\) và nhận \(\overrightarrow v = (8; - 4)\) là vectơ chỉ phương
b) Tìm tọa độ điểm P trên \(\Delta \),biết P có tung độ bằng 1.
Lời giải chi tiết:
a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = - 9 + 8t\\y = 5 - 4t\end{array} \right.\)
b) Thay \(y = 1\) vào phương trình \(y = 5 - 4t\) ta được \(1 = 5 - 4t \Rightarrow t = 1\)
Thay \(t = 1\) vào phương trình \(x = - 9 + 8t\), ta được \(x = - 1\)
Vậy \(P( - 1;1)\)
Viết phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong các trường hợp sau:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
Lời giải chi tiết:
a) Đường thẳng \(\Delta \)có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {5; - 3} \right)\), nên ta có phương trình tham số của \(\Delta \) là :
\(\left\{ \begin{array}{l}x = 1 + 5t\\y = 1 - 3t\end{array} \right.\)
Đường thẳng \(\Delta \)đi qua điểm \(A(1;1)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 1) + 5(y - 1) = 0 \Leftrightarrow 3x + 5y - 8 = 0\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = 2t\\y = - 7t\end{array} \right.\)
Đường thẳng \(\Delta \)có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {7;2} \right)\) và đi qua \(O(0;0)\)
Ta có phương trình tổng quát là
\(7(x - 0) + 2(y - 0) = 0 \Leftrightarrow 7x + 2y = 0\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {MN} = ( - 4;3)\) và có vectơ pháp tuyến \(\overrightarrow n = (3;4)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 4 - 4t\\y = 3t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(3(x - 4) + 4(x - 0) = 0 \Leftrightarrow 3x + 4y - 12 = 0\)
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình:
\(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
Phương pháp giải:
Bước 1: Tìm tọa độ điểm M qua \({M_0}\) và a,b
Bước 2: Thay vào phương trình
Lời giải chi tiết:
\(\Delta \) nhận vectơ \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến, suy ra vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = (b; - a)\)
M và \({M_0}\) thuộc đường thẳng \(\Delta \) nên \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\), suy ra \(\left\{ \begin{array}{l}{x_0} - x = b\\{y_0} - y = - a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - b\\y = {y_0} + a\end{array} \right.\)
Suy ra \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
Thay tọa độ điểm M vào phương trình \(ax + by + c = 0\) ta có:
\(a\left( {{x_0} - b} \right) + b\left( {{y_0} + a} \right) + c = \left( { - ab + ba} \right) + \left( {a{x_0} + b{y_0} + c} \right) = 0\) (đúng vì \( - a{x_0} - b{y_0} = c\))
Vậy \(M(x;y)\) thỏa mãn phương trình đã cho
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm \(M(x;y)\) từ vị trí \(A(1;2)\) chuyển động thẳng đều với Vectơ vận tốc \(\overrightarrow v = (3; - 4)\)
a) Viết phương trình tổng quát của đường thẳng \(\Delta \) biểu diễn đường đi của điểm M
b) Tìm tọa độ của điểm M khi \(\Delta \) cắt trục hoành
Phương pháp giải:
a) Từ vectơ chỉ phương tìm vectơ pháp tuyến và viết phương trình tổng quát
VTCP (a;b) => VTPT: (-b; a) hoặc (b; -a)
b) M thuộc trục hoành thì M có tọa độ (m; 0)
Lời giải chi tiết:
a) Đường thẳng \(\Delta \)có vectơ chỉ phương \(\overrightarrow v = \left( {3; - 4} \right)\),nên có vectơ pháp tuyến là \(\overrightarrow n = \left( {4;3} \right)\) và đi qua \(A(1;2)\)
Ta có phương trình tổng quát là
\(4(x - 1) + 3(y - 2) = 0 \Leftrightarrow 4x + 3y - 10 = 0\)
b) Điểm M thuộc trục hoành nên tung độ bằng 0
Thay \(y = 0\) vào phương trình \(4x + 3y - 10 = 0\) ta tìm được \(x = \frac{5}{2}\)
Vậy \(\Delta \) cắt trục hoành tại điểm \(M\left( {\frac{5}{2};0} \right)\)
Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2
Lời giải chi tiết:
a) Ta có \(3x + 5y - 8 = 0 \Leftrightarrow y = \frac{8}{5} - \frac{3}{5}x\)
Vậy hàm số bậc ứng với đường thẳng \(3x + 5y - 8 = 0\) là \(y = \frac{8}{5} - \frac{3}{5}x\)
b) Ta có \(7x + 2y = 0 \Leftrightarrow y = - \frac{7}{2}x\)
Vậy hàm số bậc ứng với đường thẳng \(7x + 2y = 0\) là \(y = - \frac{7}{2}x\)
c) Ta có \(3x + 4y - 12 = 0 \Leftrightarrow y = 3 - \frac{3}{4}x\)
Vậy hàm số bậc ứng với đường thẳng \(3x + 4y - 12 = 0\) là \(y = 3 - \frac{3}{4}x\)
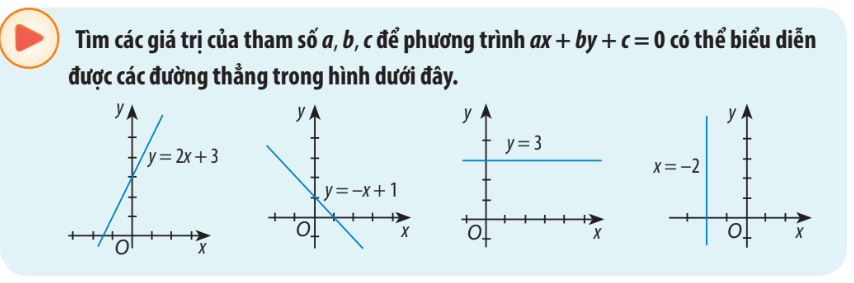
Lời giải chi tiết:
+) Hình 1: \(y = 2x + 3 \Rightarrow 2x - y + 3 = 0\)
Vậy \(a = 2,b = -1,c = 3\)
+) Hình 2: \(y = - x + 1 \Rightarrow x + y - 1 = 0\)
Vậy \(a = 1,b = 1,c = - 1\)
+) Hình 3: \(y = 3 \Rightarrow y - 3 = 0\)
Vậy \(a = 0,b = 1,c = - 3\)
+ Hình 4: \(x = - 2 \Rightarrow x + 2 = 0\)
Vậy \(a = 1,b = 0,c = 2\)
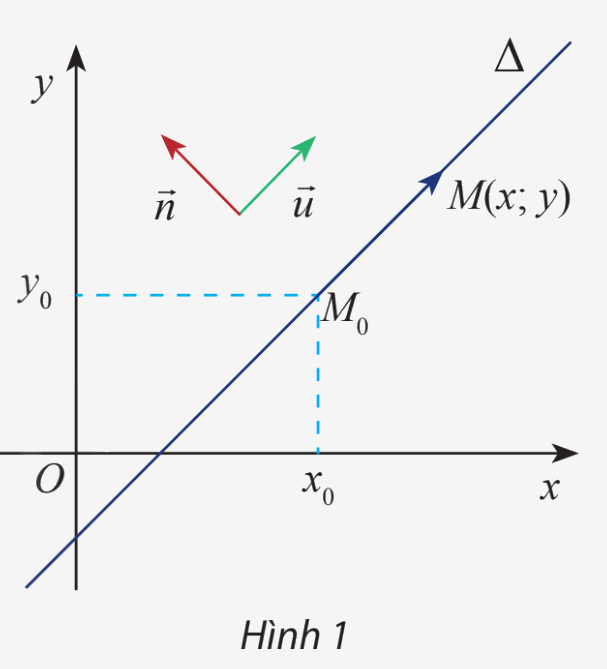
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
Phương pháp giải:
a) +) Áp dụng ứng dụng biểu thức tọa độ của vectơ tính tích vô hướng
+) Dựa vào kết quả tích vô hướng các định phương (bằng 0 thì vuông góc)
b) +) Xác định tỉ lệ giũa các tọa độ của hai vectơ để so sánh về phương
+) Tính tích vô hướng để chứng minh vuông góc
Lời giải chi tiết:
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 \({m^3}/h\) vào một cái bể đã chứa sẵn 5 \({m^3}\) nước.
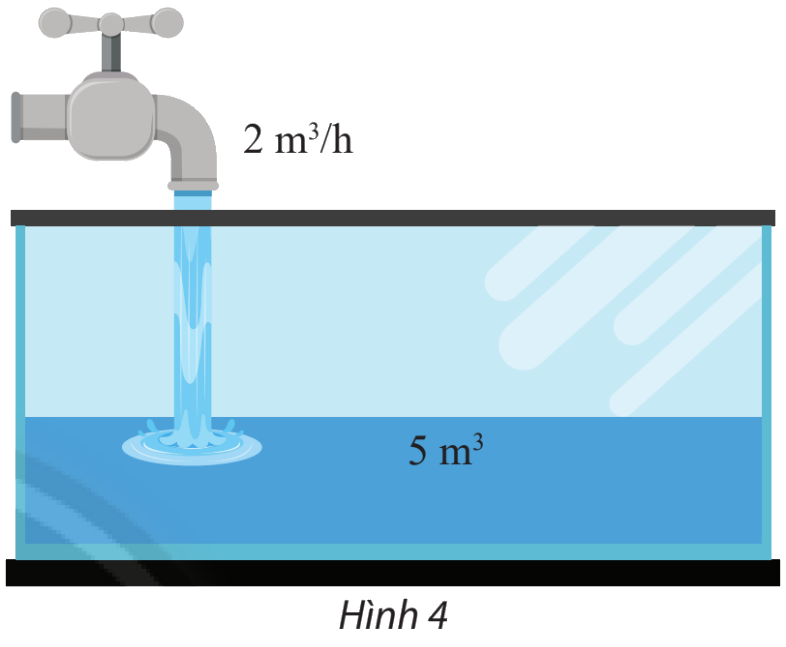
a) Viết biểu thức tính thể tích ycủa nước có trong bể sau x giờ
b) Gọi \(y = f(x)\)là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d
Lời giải chi tiết:
a) Thể tích nước trong bể được tính bằng công thức \(y = 5 + 2x\)
b)
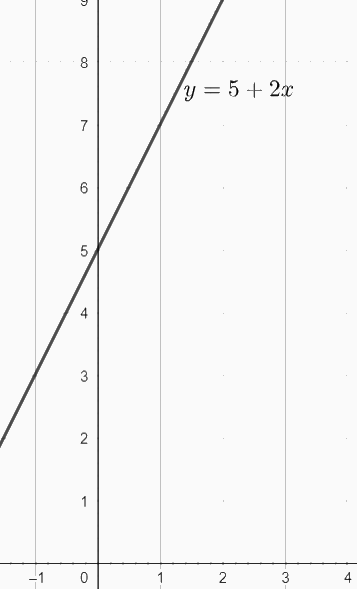
c) Ta có đồ thị hàm số bậc nhất \(y = 5 + 2x \Leftrightarrow 2x - y + 5 = 0\)
Vậy phương trình tổng quát của đường thẳng d là \(2x - y + 5 = 0\)
Từ phương trình tổng quát ta có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1} \right)\), từ đó ta có vectơ chỉ phương \(\overrightarrow u = (1;2)\)
Khi \(x = 0\) thì \(y = 5\) nên đường thẳng đó đi qua điểm \((0;5)\)
Ta có phương trình tham số của đường thẳng d là \(\left\{ \begin{array}{l}x = t\\y = 5 + 2t\end{array} \right.\)
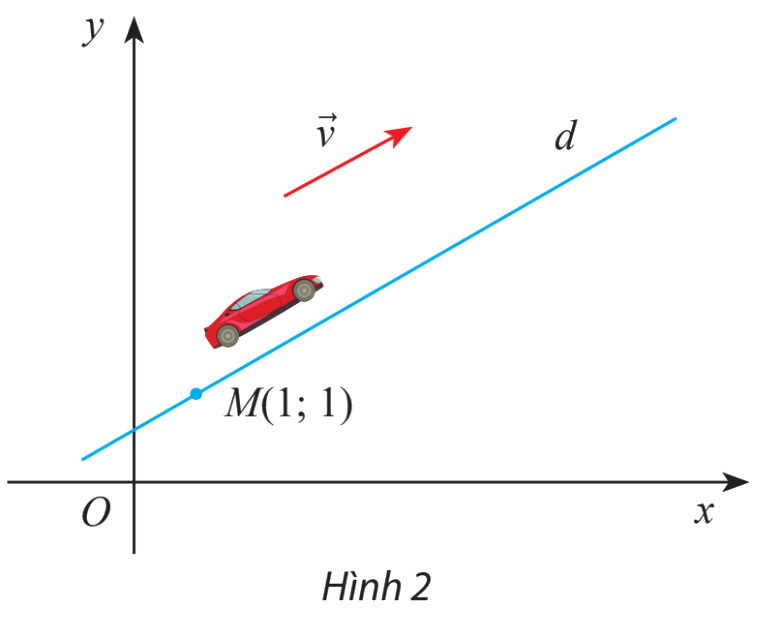
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với Vectơ vận tốc\(\overrightarrow v = (40;30)\)
a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô
b) Tìm tọa độ của xe tương ứng với t = 2; t = 4
Lời giải chi tiết:
a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)
Lời giải chi tiết:
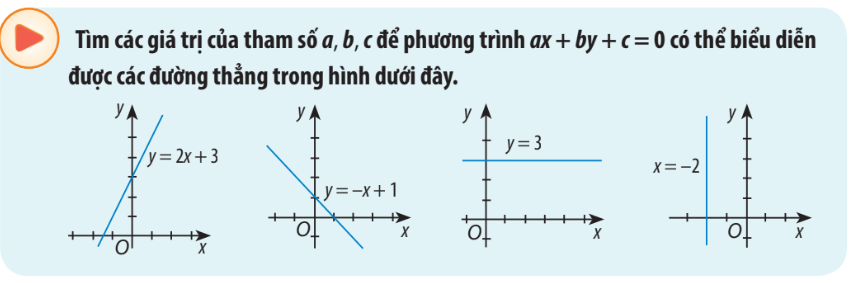
+) Hình 1: \(y = 2x + 3 \Rightarrow 2x - y + 3 = 0\)
Vậy \(a = 2,b = -1,c = 3\)
+) Hình 2: \(y = - x + 1 \Rightarrow x + y - 1 = 0\)
Vậy \(a = 1,b = 1,c = - 1\)
+) Hình 3: \(y = 3 \Rightarrow y - 3 = 0\)
Vậy \(a = 0,b = 1,c = - 3\)
+ Hình 4: \(x = - 2 \Rightarrow x + 2 = 0\)
Vậy \(a = 1,b = 0,c = 2\)
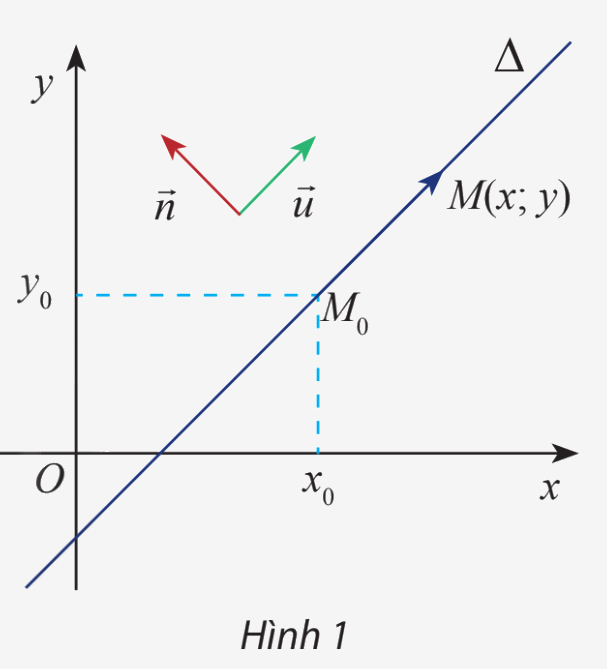
Trong mặt phẳng Oxy, cho hai đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và vectơ \(\overrightarrow n = \left( {a;b} \right)\) và \(\overrightarrow u = \left( {b; - a} \right)\) khác vectơ 0. Cho biết \(\overrightarrow u \) có giá song song hoặc trùng với \(\Delta \).
a) Tính tích vô hướng \(\overrightarrow n \overrightarrow {.u} \) và nêu nhận xét về phương của hai vectơ \(\overrightarrow n ,\overrightarrow u \)
b) Gọi \(M\left( {x;y} \right)\) là điểm di động trên \(\Delta \). Chứng tỏ rằng vectơ \(\overrightarrow {{M_0}M} \) luôn cùng phương với vectơ \(\overrightarrow u \) và luôn vuông góc với vectơ \(\overrightarrow n \)
Phương pháp giải:
a) +) Áp dụng ứng dụng biểu thức tọa độ của vectơ tính tích vô hướng
+) Dựa vào kết quả tích vô hướng các định phương (bằng 0 thì vuông góc)
b) +) Xác định tỉ lệ giũa các tọa độ của hai vectơ để so sánh về phương
+) Tính tích vô hướng để chứng minh vuông góc
Lời giải chi tiết:
a) Ta có \(\overrightarrow n .\overrightarrow u = a.b + b.( - a) = 0\)
Tích vô hướng bằng 0 nên hai vectơ \(\overrightarrow n ,\overrightarrow u \)có phương vuông góc với nhau
b) Vectơ \(\overrightarrow {{M_0}M} \) có giá là đường thẳng \(\Delta\)
=> luôn cùng phương với vectơ \(\overrightarrow u \)
=> vectơ \(\overrightarrow {{M_0}M} \) có phương vuông góc với vectơ \(\overrightarrow n \)
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow u = \left( {{u_1};{u_2}} \right)\) là vectơ chỉ phương. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), tìm tọa độ của điểm M theo tọa độ của \({M_0}\) và \(\overrightarrow u \)
Phương pháp giải:
M và \({M_0}\) thuộc \(\Delta \) nên \({\overrightarrow {MM} _0}\) làm vectơ chỉ phương
Lời giải chi tiết:
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\) mà \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương nên ta có:
\(\left\{ \begin{array}{l}{x_0} - x = {u_1}\\{y_0} - y = {u_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - {u_1}\\y = {y_0} - {u_2}\end{array} \right.\)
Vậy \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
a) Viết phương trình tham số của đường thẳng d đi qua điểm \(B( - 9;5)\) và nhận \(\overrightarrow v = (8; - 4)\) là vectơ chỉ phương
b) Tìm tọa độ điểm P trên \(\Delta \),biết P có tung độ bằng 1.
Lời giải chi tiết:
a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = - 9 + 8t\\y = 5 - 4t\end{array} \right.\)
b) Thay \(y = 1\) vào phương trình \(y = 5 - 4t\) ta được \(1 = 5 - 4t \Rightarrow t = 1\)
Thay \(t = 1\) vào phương trình \(x = - 9 + 8t\), ta được \(x = - 1\)
Vậy \(P( - 1;1)\)
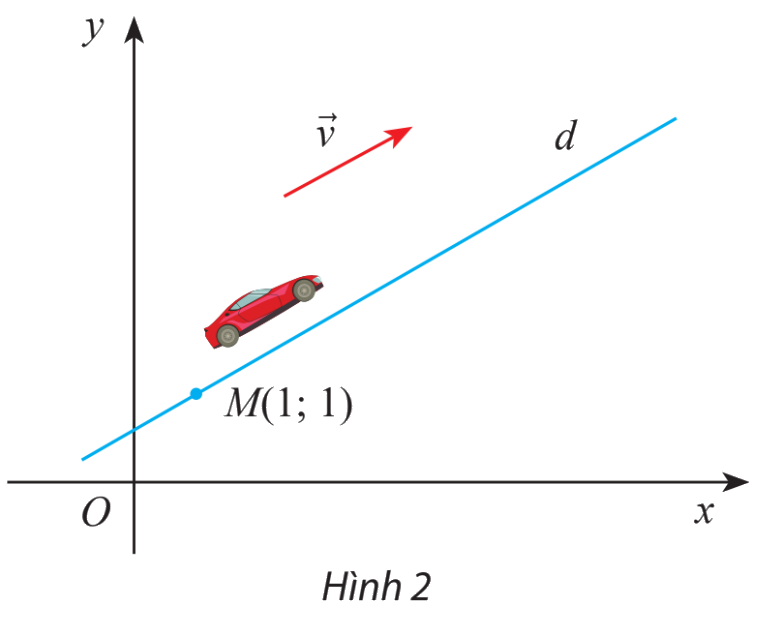
Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm \(M(1;1)\) với Vectơ vận tốc\(\overrightarrow v = (40;30)\)
a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô
b) Tìm tọa độ của xe tương ứng với t = 2; t = 4
Lời giải chi tiết:
a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)
Trong mặt phẳng Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến. Với mỗi điểm \(M\left( {x;y} \right)\) thuộc \(\Delta \), chứng tỏ rằng điểm \(M\left( {x;y} \right)\) có tọa độ thỏa mãn phương trình:
\(ax + by + c = 0\) (với \(c = - a{x_0} - b{y_0}\))
Phương pháp giải:
Bước 1: Tìm tọa độ điểm M qua \({M_0}\) và a,b
Bước 2: Thay vào phương trình
Lời giải chi tiết:
\(\Delta \) nhận vectơ \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến, suy ra vectơ chỉ phương của \(\Delta \) là \(\overrightarrow u = (b; - a)\)
M và \({M_0}\) thuộc đường thẳng \(\Delta \) nên \(\Delta \) nhận \({\overrightarrow {MM} _0}\)làm vectơ chỉ phương
\({\overrightarrow {MM} _0} = \left( {{x_0} - x;{y_0} - y} \right)\), suy ra \(\left\{ \begin{array}{l}{x_0} - x = b\\{y_0} - y = - a\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = {x_0} - b\\y = {y_0} + a\end{array} \right.\)
Suy ra \(M\left( {{x_0} - {u_1};{y_0} - {u_2}} \right)\)
Thay tọa độ điểm M vào phương trình \(ax + by + c = 0\) ta có:
\(a\left( {{x_0} - b} \right) + b\left( {{y_0} + a} \right) + c = \left( { - ab + ba} \right) + \left( {a{x_0} + b{y_0} + c} \right) = 0\) (đúng vì \( - a{x_0} - b{y_0} = c\))
Vậy \(M(x;y)\) thỏa mãn phương trình đã cho
Viết phương trình tham số và phương trình tổng quát của đường thẳng \(\Delta \) trong các trường hợp sau:
a) Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\)và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\)
Lời giải chi tiết:
a) Đường thẳng \(\Delta \)có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {5; - 3} \right)\), nên ta có phương trình tham số của \(\Delta \) là :
\(\left\{ \begin{array}{l}x = 1 + 5t\\y = 1 - 3t\end{array} \right.\)
Đường thẳng \(\Delta \)đi qua điểm \(A(1;1)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 1) + 5(y - 1) = 0 \Leftrightarrow 3x + 5y - 8 = 0\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = 2t\\y = - 7t\end{array} \right.\)
Đường thẳng \(\Delta \)có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {7;2} \right)\) và đi qua \(O(0;0)\)
Ta có phương trình tổng quát là
\(7(x - 0) + 2(y - 0) = 0 \Leftrightarrow 7x + 2y = 0\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {MN} = ( - 4;3)\) và có vectơ pháp tuyến \(\overrightarrow n = (3;4)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 4 - 4t\\y = 3t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(3(x - 4) + 4(x - 0) = 0 \Leftrightarrow 3x + 4y - 12 = 0\)
Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm \(M(x;y)\) từ vị trí \(A(1;2)\) chuyển động thẳng đều với Vectơ vận tốc \(\overrightarrow v = (3; - 4)\)
a) Viết phương trình tổng quát của đường thẳng \(\Delta \) biểu diễn đường đi của điểm M
b) Tìm tọa độ của điểm M khi \(\Delta \) cắt trục hoành
Phương pháp giải:
a) Từ vectơ chỉ phương tìm vectơ pháp tuyến và viết phương trình tổng quát
VTCP (a;b) => VTPT: (-b; a) hoặc (b; -a)
b) M thuộc trục hoành thì M có tọa độ (m; 0)
Lời giải chi tiết:
a) Đường thẳng \(\Delta \)có vectơ chỉ phương \(\overrightarrow v = \left( {3; - 4} \right)\),nên có vectơ pháp tuyến là \(\overrightarrow n = \left( {4;3} \right)\) và đi qua \(A(1;2)\)
Ta có phương trình tổng quát là
\(4(x - 1) + 3(y - 2) = 0 \Leftrightarrow 4x + 3y - 10 = 0\)
b) Điểm M thuộc trục hoành nên tung độ bằng 0
Thay \(y = 0\) vào phương trình \(4x + 3y - 10 = 0\) ta tìm được \(x = \frac{5}{2}\)
Vậy \(\Delta \) cắt trục hoành tại điểm \(M\left( {\frac{5}{2};0} \right)\)
Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2
Lời giải chi tiết:
a) Ta có \(3x + 5y - 8 = 0 \Leftrightarrow y = \frac{8}{5} - \frac{3}{5}x\)
Vậy hàm số bậc ứng với đường thẳng \(3x + 5y - 8 = 0\) là \(y = \frac{8}{5} - \frac{3}{5}x\)
b) Ta có \(7x + 2y = 0 \Leftrightarrow y = - \frac{7}{2}x\)
Vậy hàm số bậc ứng với đường thẳng \(7x + 2y = 0\) là \(y = - \frac{7}{2}x\)
c) Ta có \(3x + 4y - 12 = 0 \Leftrightarrow y = 3 - \frac{3}{4}x\)
Vậy hàm số bậc ứng với đường thẳng \(3x + 4y - 12 = 0\) là \(y = 3 - \frac{3}{4}x\)
Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 \({m^3}/h\) vào một cái bể đã chứa sẵn 5 \({m^3}\) nước.
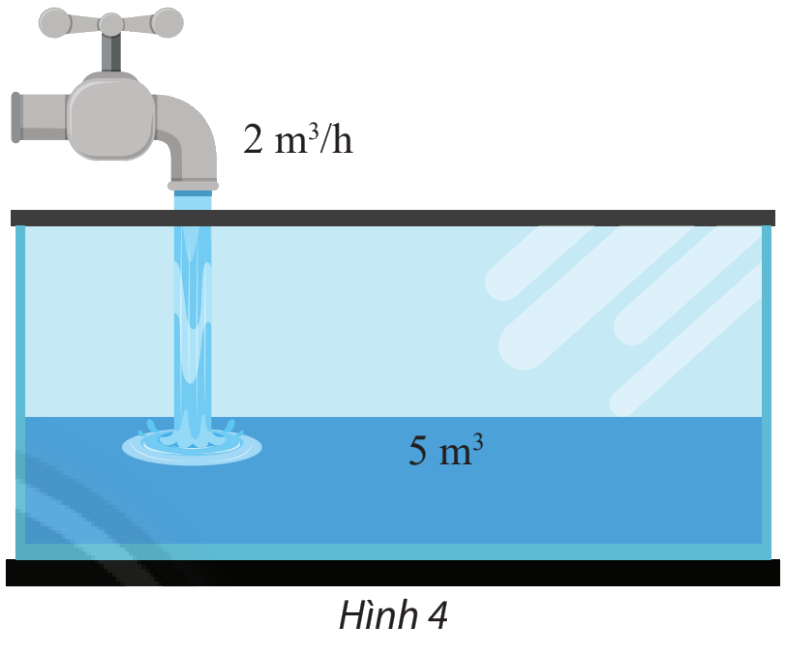
a) Viết biểu thức tính thể tích ycủa nước có trong bể sau x giờ
b) Gọi \(y = f(x)\)là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d
Lời giải chi tiết:
a) Thể tích nước trong bể được tính bằng công thức \(y = 5 + 2x\)
b)
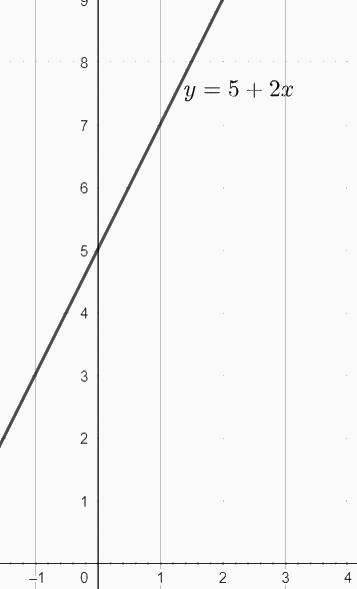
c) Ta có đồ thị hàm số bậc nhất \(y = 5 + 2x \Leftrightarrow 2x - y + 5 = 0\)
Vậy phương trình tổng quát của đường thẳng d là \(2x - y + 5 = 0\)
Từ phương trình tổng quát ta có vectơ pháp tuyến \(\overrightarrow n = \left( {2; - 1} \right)\), từ đó ta có vectơ chỉ phương \(\overrightarrow u = (1;2)\)
Khi \(x = 0\) thì \(y = 5\) nên đường thẳng đó đi qua điểm \((0;5)\)
Ta có phương trình tham số của đường thẳng d là \(\left\{ \begin{array}{l}x = t\\y = 5 + 2t\end{array} \right.\)
Mục 1 của SGK Toán 10 tập 2 chương trình Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về vectơ. Các bài tập trong mục này yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và ứng dụng của vectơ trong hình học.
Các bài tập trên trang 46 tập trung vào việc rèn luyện kỹ năng thực hiện phép cộng và phép trừ vectơ. Học sinh cần nắm vững quy tắc cộng, trừ vectơ và áp dụng vào giải các bài toán cụ thể. Ví dụ, cho hai vectơ a và b, tìm vectơ a + b hoặc a - b khi biết tọa độ của a và b.
Trang 47 yêu cầu học sinh thực hành phép nhân vectơ với một số thực. Học sinh cần hiểu rõ quy tắc nhân vectơ với một số thực và áp dụng vào giải các bài toán liên quan đến việc tìm vectơ kết quả sau phép nhân. Ví dụ, cho vectơ a và số thực k, tìm vectơ k.a.
Các trang 48 và 49 là nơi học sinh được vận dụng tất cả các kiến thức đã học về các phép toán vectơ để giải các bài toán phức tạp hơn. Các bài toán này thường yêu cầu học sinh kết hợp nhiều phép toán vectơ để tìm ra kết quả cuối cùng. Ví dụ, cho các vectơ a, b và số thực k, tính 2a + 3b - k.a.
Trang 50 và 51 tập trung vào việc ứng dụng vectơ để giải các bài toán hình học. Học sinh cần sử dụng vectơ để chứng minh các tính chất hình học, tìm tọa độ của các điểm, hoặc tính độ dài của các đoạn thẳng. Ví dụ, chứng minh rằng tứ giác ABCD là hình bình hành bằng phương pháp vectơ.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong mục 1 trang 46, 47, 48, 49, 50, 51 SGK Toán 10 tập 2 Chân trời sáng tạo. Các lời giải này được trình bày một cách rõ ràng, logic, giúp học sinh dễ dàng theo dõi và hiểu được phương pháp giải.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Chúng tôi cam kết mang đến cho học sinh một trải nghiệm học tập hiệu quả, thú vị và thành công.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng vectơ |
| (a + b) + c = a + (b + c) | Tính kết hợp của phép cộng vectơ |
| k(a + b) = ka + kb | Tính chất phân phối của phép nhân với phép cộng vectơ |