Bài 7 trang 73 SGK Toán 10 tập 1 thuộc chương trình học Toán 10 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Bài tập này giúp củng cố lý thuyết và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7 trang 73 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27. a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC. b) Tính diện tích tam giác GBC.
Đề bài
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
Phương pháp giải - Xem chi tiết
a) Tính r bằng công thức: \(S = p.r\). Trong đó S tính bởi công thức heron.
b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC
Lời giải chi tiết
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
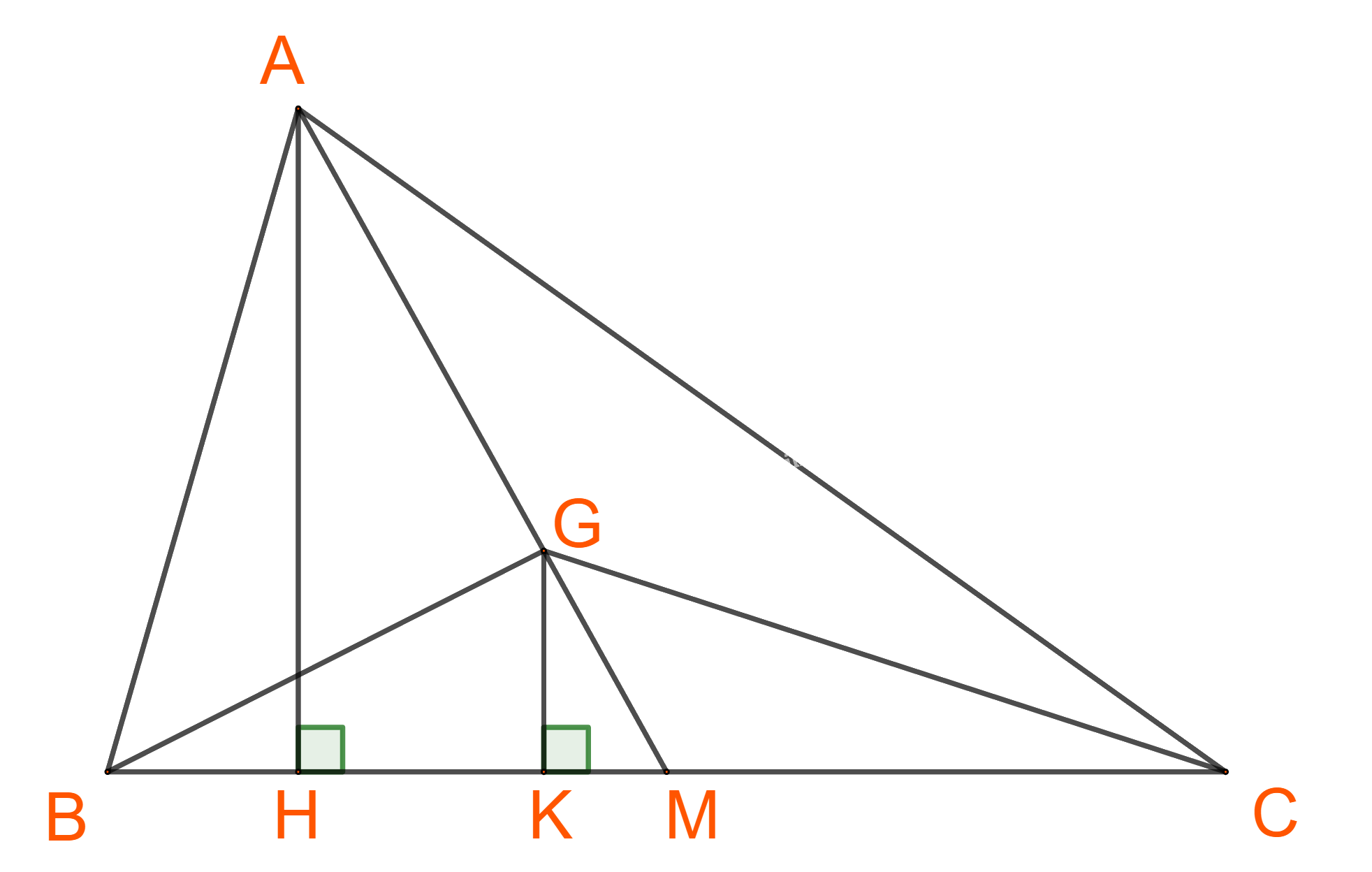
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)
Bài 7 trang 73 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc ứng dụng các kiến thức về vectơ trong hình học. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài tập 7 yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh một số đẳng thức vectơ liên quan đến các điểm trong hình học. Cụ thể, bài tập thường yêu cầu chứng minh một điểm là trung điểm của một đoạn thẳng, hoặc chứng minh ba điểm thẳng hàng.
Để giải bài tập 7 trang 73 SGK Toán 10 tập 1, học sinh có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho bài tập 7, bao gồm các bước giải, giải thích rõ ràng và hình vẽ minh họa nếu cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.)
Ví dụ 1: Cho tam giác ABC, M là trung điểm của BC. Chứng minh rằng overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2.
Giải:
Vì M là trung điểm của BC, ta có overrightarrow{BM} =overrightarrow{MC}. Do đó, overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM} =overrightarrow{AB} +overrightarrow{MC} =overrightarrow{AB} + (overrightarrow{AC} -overrightarrow{AM}). Suy ra 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}, hay overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2.
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh có thể tự giải các bài tập sau:
Bài 7 trang 73 SGK Toán 10 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về vectơ. Bằng cách nắm vững lý thuyết, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.