Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 6, 7 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả cao trong học tập.
Đồ thị của hàm số y= f(x) được biểu diễn trong hình 1 Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x=1 Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
a) \(f\left( x \right) = 2{x^2} - 5x + 2\)
b) \(g\left( x \right) = - {x^2} + 6x - 9\)
c) \(h\left( x \right) = 4{x^2} - 4x + 9\)
Phương pháp giải:
Bước 1: Xác định biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xét dấu của \(\Delta \)
Bước 3: Tìm nghiệm
+) Nếu \(\Delta > 0 \Rightarrow {x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\)
+) Nếu \(\Delta = 0 \Rightarrow {x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
+) Nếu \(\Delta = 0\)thì tam thức bậc hai vô nghiệm
Lời giải chi tiết:
a) Tam thức bậc hai \(f\left( x \right) = 2{x^2} - 5x + 2\) có \(\Delta = {\left( { - 5} \right)^2} - 4.2.2 = 9\)
\(\Delta > 0\), do đó \(f\left( x \right)\) có hai nghiệm phân biệt là
\({x_1} = \frac{{5 + \sqrt 9 }}{4} = 2\) và \({x_1} = \frac{{5 - \sqrt 9 }}{4} = \frac{1}{2}\)
b) Tam thức bậc hai \(g\left( x \right) = - {x^2} + 6x - 9\) có \(\Delta = {6^2} - 4.\left( { - 1} \right).\left( { - 9} \right) = 0\)
\(\Delta = 0\), do đó \(g\left( x \right)\)có nghiệm kép \({x_1} = {x_2} = \frac{{ - 6}}{{2.\left( { - 1} \right)}} = 3\)
c) Tam thức bậc hai \(h\left( x \right) = 4{x^2} - 4x + 9\) có \(\Delta = {\left( { - 4} \right)^2} - 4.4.9 = - 128\)
\(\Delta < 0\), do đó \(h\left( x \right)\) vô nghiệm
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).
a) \(f\left( x \right) = 2{x^2} + x - 1\);
b) \(g\left( x \right) = - {x^4} + 2{x^2} + 1\)
c) \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\)
Lời giải chi tiết:
a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)
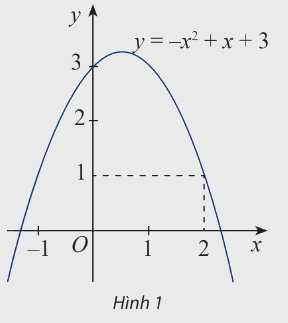
Đồ thị của hàm số \(y = f\left( x \right) = - {x^2} + x + 3\)được biểu diễn trong hình 1
a) Biểu thức \(f\left( x \right)\) là đa thức bậc mấy?
b) Xác định dấu của \(f\left( 2 \right)\)
Phương pháp giải:
a) Xác định số mũ cao nhất
b) Thay \(x = 2\) vào \(f\left( x \right)\), so sánh với 0.
Lời giải chi tiết:
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai
b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:
\(f\left( 2 \right) = - {2^2} + 2 + 3 = 1 > 0\)
Suy ra \(f\left( 2 \right)\) dương.
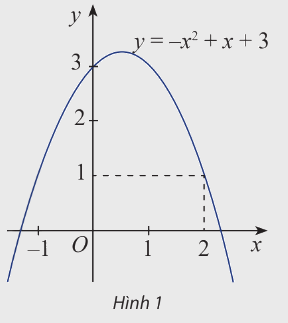
Đồ thị của hàm số \(y = f\left( x \right) = - {x^2} + x + 3\)được biểu diễn trong hình 1
a) Biểu thức \(f\left( x \right)\) là đa thức bậc mấy?
b) Xác định dấu của \(f\left( 2 \right)\)
Phương pháp giải:
a) Xác định số mũ cao nhất
b) Thay \(x = 2\) vào \(f\left( x \right)\), so sánh với 0.
Lời giải chi tiết:
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai
b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:
\(f\left( 2 \right) = - {2^2} + 2 + 3 = 1 > 0\)
Suy ra \(f\left( 2 \right)\) dương.
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại \(x = 1\).
a) \(f\left( x \right) = 2{x^2} + x - 1\);
b) \(g\left( x \right) = - {x^4} + 2{x^2} + 1\)
c) \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\)
Lời giải chi tiết:
a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)
Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
a) \(f\left( x \right) = 2{x^2} - 5x + 2\)
b) \(g\left( x \right) = - {x^2} + 6x - 9\)
c) \(h\left( x \right) = 4{x^2} - 4x + 9\)
Phương pháp giải:
Bước 1: Xác định biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Xét dấu của \(\Delta \)
Bước 3: Tìm nghiệm
+) Nếu \(\Delta > 0 \Rightarrow {x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\)
+) Nếu \(\Delta = 0 \Rightarrow {x_1} = {x_2} = \frac{{ - b}}{{2a}}\)
+) Nếu \(\Delta = 0\)thì tam thức bậc hai vô nghiệm
Lời giải chi tiết:
a) Tam thức bậc hai \(f\left( x \right) = 2{x^2} - 5x + 2\) có \(\Delta = {\left( { - 5} \right)^2} - 4.2.2 = 9\)
\(\Delta > 0\), do đó \(f\left( x \right)\) có hai nghiệm phân biệt là
\({x_1} = \frac{{5 + \sqrt 9 }}{4} = 2\) và \({x_1} = \frac{{5 - \sqrt 9 }}{4} = \frac{1}{2}\)
b) Tam thức bậc hai \(g\left( x \right) = - {x^2} + 6x - 9\) có \(\Delta = {6^2} - 4.\left( { - 1} \right).\left( { - 9} \right) = 0\)
\(\Delta = 0\), do đó \(g\left( x \right)\)có nghiệm kép \({x_1} = {x_2} = \frac{{ - 6}}{{2.\left( { - 1} \right)}} = 3\)
c) Tam thức bậc hai \(h\left( x \right) = 4{x^2} - 4x + 9\) có \(\Delta = {\left( { - 4} \right)^2} - 4.4.9 = - 128\)
\(\Delta < 0\), do đó \(h\left( x \right)\) vô nghiệm
Mục 1 của SGK Toán 10 tập 2 chương trình Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về vectơ. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ để giải quyết các bài toán hình học và đại số cơ bản. Việc nắm vững kiến thức nền tảng và rèn luyện kỹ năng giải bài tập là vô cùng quan trọng để các em có thể tiếp thu tốt các kiến thức mới trong chương trình học.
Bài tập mục 1 trang 6, 7 SGK Toán 10 tập 2 Chân trời sáng tạo bao gồm các dạng bài tập sau:
Để giải bài tập này, các em cần nắm vững định nghĩa của vectơ và cách biểu diễn vectơ bằng tọa độ. Ví dụ, để tìm vectơ AB, ta lấy tọa độ của điểm B trừ đi tọa độ của điểm A.
Để giải bài tập này, các em cần thực hiện phép cộng vectơ trước, sau đó tính độ dài của vectơ kết quả. Độ dài của vectơ (x; y) được tính bằng công thức √(x² + y²).
Để giải bài tập này, các em cần thực hiện phép nhân vectơ với một số thực, sau đó thực hiện phép trừ vectơ. Phép nhân vectơ với một số thực được thực hiện bằng cách nhân mỗi thành phần của vectơ với số thực đó.
Để giải bài tập vectơ một cách hiệu quả, các em cần:
Vectơ có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc học tập môn Toán 10. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả cao trong các kỳ thi sắp tới. Chúc các em học tốt!