Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 1 trang 12 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong môn Toán.
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
Đề bài
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
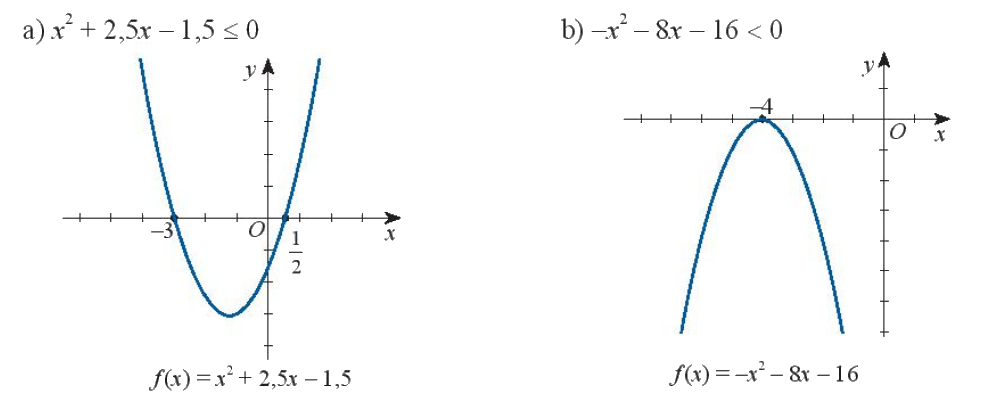
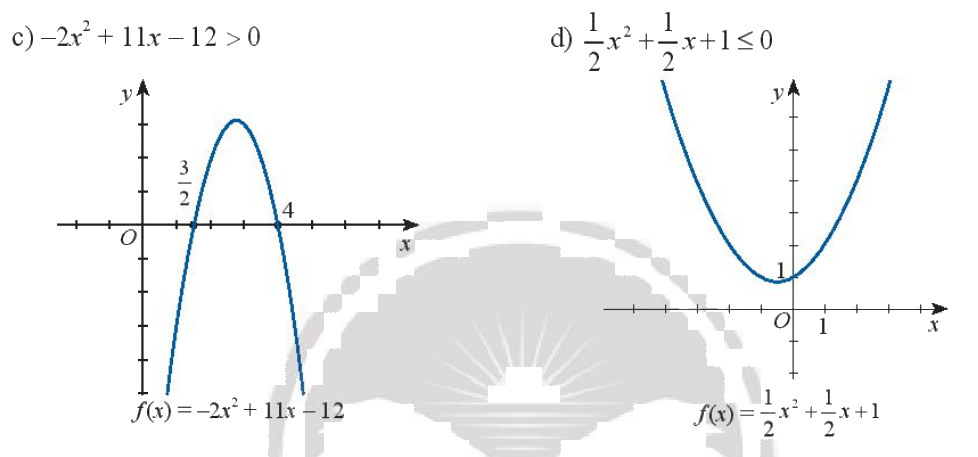
Phương pháp giải - Xem chi tiết
+) Phần đồ thị nằm trên trục hoành có các x tương ứng là nghiệm của BPT \(f\left( x \right) > 0\)
+) Phần đồ thị nằm dưới trục hoành có các x tương ứng là nghiệm của BPT \(f\left( x \right) < 0\)
+) Tại x có đồ thị cắt trục hoành là nghiệm của BPT \(f\left( x \right) = 0\)
Lời giải chi tiết
a) Dựa vào đồ thị ta thấy \({x^2} + 2,5x - 1,5 \le 0\) khi x thuộc đoạn \(\left[ { - 3;\frac{1}{2}} \right]\)
Vậy nghiệm của bất phương trình \({x^2} + 2,5x - 1,5 \le 0\) là \(\left[ { - 3;\frac{1}{2}} \right]\)
b) Dựa vào đồ thị ta thấy \( - {x^2} - 8x - 16 < 0\) với mọi x khác \( - 4\)
Vậy nghiệm của bất phương trình \( - {x^2} - 8x - 16 < 0\) là \(\mathbb{R}\backslash \left\{ { - 4} \right\}\)
c) Dựa vào đồ thị ta thấy \( - 2{x^2} + 11x - 12 > 0\) khi x thuộc khoảng \(\left( {\frac{3}{2};4} \right)\)
Vậy nghiệm của bất phương trình \( - 2{x^2} + 11x - 12 > 0\) là \(\left( {\frac{3}{2};4} \right)\)
d) Dựa vào đồ thị ta thấy đồ thị của tam thức \(f\left( x \right) = \frac{1}{2}{x^2} + \frac{1}{2}x + 1\) nằm hoàn toàn phía trên trục hoành với mọi x
Vậy bất phương trình \(\frac{1}{2}{x^2} + \frac{1}{2}x + 1 \le 0\) vô nghiệm.
Bài 1 trang 12 SGK Toán 10 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 10, tập trung vào việc ôn tập chương 3: Hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, bao gồm các yếu tố như hệ số a, b, c, đỉnh của parabol, trục đối xứng, và khoảng đồng biến, nghịch biến để giải quyết các bài toán cụ thể.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 12 SGK Toán 10 tập 2 – Chân trời sáng tạo một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Bài tập: Cho hàm số y = 2x2 - 4x + 1. Hãy xác định hệ số a, b, c, tọa độ đỉnh của parabol, trục đối xứng và khoảng đồng biến, nghịch biến của hàm số.
Giải:
Khi giải bài tập về hàm số bậc hai, bạn cần lưu ý những điều sau:
Bài 1 trang 12 SGK Toán 10 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Bằng cách nắm vững lý thuyết, áp dụng phương pháp giải phù hợp và luyện tập thường xuyên, bạn có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!
| Công thức | Mô tả |
|---|---|
| xđỉnh = -b / (2a) | Hoành độ đỉnh của parabol |
| yđỉnh = f(xđỉnh) | Tung độ đỉnh của parabol |