Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 40, 41 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 10 và đạt kết quả tốt nhất trong học tập.
Một thiết bị thăm dò đáy biển đang lặn với vận tốc v=(10; - 8) (hình 8).
Trong mặt phẳng Oxy, cho hai vectơ \(\overrightarrow a = \left( {{a_1},{a_2}} \right),\overrightarrow b = \left( {{b_1},{b_2}} \right)\) và số thực k. Ta đã biết có thể biểu diễn từng vectơ \(\overrightarrow a ,\overrightarrow b \) theo hai vectơ , \(\overrightarrow j \) như sau
a) Biểu diễn từng vectơ \(\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,k\overrightarrow a \) theo hai vectơ , \(\overrightarrow j \)
b) Tìm \(\overrightarrow a .\overrightarrow b \) theo tọa độ của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
Lời giải chi tiết:
a) Ta có
\(\begin{array}{*{20}{l}}{\vec a + \vec b = \left( {{a_1} + {a_2}\vec j} \right) + \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} + {b_1}} \right) + \left( {{a_2} + {b_2}} \right)}\\{\vec a - \vec b = \left( {{a_1} + {a_2}\vec j} \right) - \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} - {b_1}} \right) + \left( {{a_2} - {b_2}} \right)}\\{k\vec a = k\left( {{a_1} + {a_2}\vec j} \right) = k{a_1} + k{a_2}\vec j}\end{array}\)
b) Ta có
\(\begin{array}{l}\vec a.\vec b = \left( {{a_1}\overrightarrow i + {a_2}\vec j} \right).\left( {{b_1}\overrightarrow i + {b_2}\vec j} \right)\\ = {a_1}{b_1}{\overrightarrow i ^2} + {a_1}{b_2}\overrightarrow i .\vec j + {a_2}{b_1}\overrightarrow i \vec j + {a_2}{b_2}{{\vec j}^2}\\ = {a_1}{b_1} + {a_2}{b_2}\end{array}\)
Vì \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1,{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2} = 1,\overrightarrow i \overrightarrow j = 0\)
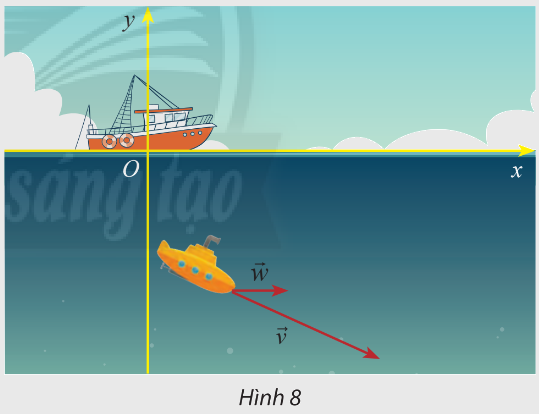
Một thiết bị thăm dò đáy biển đang lặn với vận tốc \(\overrightarrow v = \left( {10; - 8} \right)\) (hình 8). Cho biết vận tốc của dòng hải lưu vùng biển là \(\overrightarrow w = \left( {3,5;0} \right)\). Tìm tọa dộ của vectơ tổng hai vận tốc \(\overrightarrow v \) và \(\overrightarrow w \)
Phương pháp giải:
Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)
Lời giải chi tiết:
\(\overrightarrow v + \overrightarrow w = (10 + 3,5;( - 8) + 0) = (13,5; - 8)\)
Vậy tọa độ của vectơ tổng hai vận tốc \(\overrightarrow v \) và \(\overrightarrow w \) là \((13,5; - 8)\)
Cho hai vectơ \(\overrightarrow m = \left( { - 6;1} \right),\overrightarrow n = \left( {0;2} \right)\)
a) Tìm tọa độ các vectơ \(\overrightarrow m + \overrightarrow n ,\overrightarrow m - \overrightarrow n ,10\overrightarrow m , - 4\overrightarrow n \)
b) Tính các tích vô hướng \(\overrightarrow m .\overrightarrow n ,\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right)\)
Phương pháp giải:
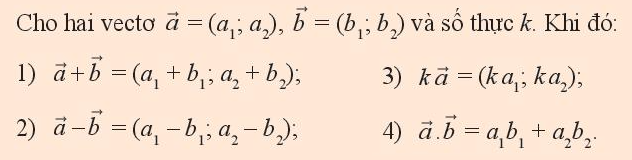
Lời giải chi tiết:
a) Ta có
\(\begin{array}{l}\overrightarrow m + \overrightarrow n = \left( {\left( { - 6 + 0} \right);1 + 2} \right) = ( - 6;3)\\\overrightarrow m - \overrightarrow n = \left( {\left( { - 6 - 0} \right);\left( {1 - 2} \right)} \right) = \left( { - 6; - 1} \right)\\10\overrightarrow m = (10.( - 6);10.1) = ( - 60;10)\\ - 4\overrightarrow n = (( - 4).0;( - 4).2) = (0; - 8)\end{array}\)
b) Ta có
\(\overrightarrow m .\overrightarrow n = ( - 6).0 + 1.2 = 0 + 2 = 2\)
Ta có \(10\overrightarrow m = ( - 60;10)\) và \( - 4\overrightarrow n = (0; - 8)\) nên \(\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right) = ( - 60).0 + 10.( - 8) = 0 - 80 = - 80\)
Trong mặt phẳng Oxy, cho hai vectơ \(\overrightarrow a = \left( {{a_1},{a_2}} \right),\overrightarrow b = \left( {{b_1},{b_2}} \right)\) và số thực k. Ta đã biết có thể biểu diễn từng vectơ \(\overrightarrow a ,\overrightarrow b \) theo hai vectơ , \(\overrightarrow j \) như sau
a) Biểu diễn từng vectơ \(\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,k\overrightarrow a \) theo hai vectơ , \(\overrightarrow j \)
b) Tìm \(\overrightarrow a .\overrightarrow b \) theo tọa độ của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
Lời giải chi tiết:
a) Ta có
\(\begin{array}{*{20}{l}}{\vec a + \vec b = \left( {{a_1} + {a_2}\vec j} \right) + \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} + {b_1}} \right) + \left( {{a_2} + {b_2}} \right)}\\{\vec a - \vec b = \left( {{a_1} + {a_2}\vec j} \right) - \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} - {b_1}} \right) + \left( {{a_2} - {b_2}} \right)}\\{k\vec a = k\left( {{a_1} + {a_2}\vec j} \right) = k{a_1} + k{a_2}\vec j}\end{array}\)
b) Ta có
\(\begin{array}{l}\vec a.\vec b = \left( {{a_1}\overrightarrow i + {a_2}\vec j} \right).\left( {{b_1}\overrightarrow i + {b_2}\vec j} \right)\\ = {a_1}{b_1}{\overrightarrow i ^2} + {a_1}{b_2}\overrightarrow i .\vec j + {a_2}{b_1}\overrightarrow i \vec j + {a_2}{b_2}{{\vec j}^2}\\ = {a_1}{b_1} + {a_2}{b_2}\end{array}\)
Vì \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1,{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2} = 1,\overrightarrow i \overrightarrow j = 0\)
Cho hai vectơ \(\overrightarrow m = \left( { - 6;1} \right),\overrightarrow n = \left( {0;2} \right)\)
a) Tìm tọa độ các vectơ \(\overrightarrow m + \overrightarrow n ,\overrightarrow m - \overrightarrow n ,10\overrightarrow m , - 4\overrightarrow n \)
b) Tính các tích vô hướng \(\overrightarrow m .\overrightarrow n ,\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right)\)
Phương pháp giải:
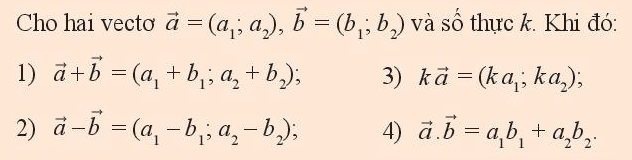
Lời giải chi tiết:
a) Ta có
\(\begin{array}{l}\overrightarrow m + \overrightarrow n = \left( {\left( { - 6 + 0} \right);1 + 2} \right) = ( - 6;3)\\\overrightarrow m - \overrightarrow n = \left( {\left( { - 6 - 0} \right);\left( {1 - 2} \right)} \right) = \left( { - 6; - 1} \right)\\10\overrightarrow m = (10.( - 6);10.1) = ( - 60;10)\\ - 4\overrightarrow n = (( - 4).0;( - 4).2) = (0; - 8)\end{array}\)
b) Ta có
\(\overrightarrow m .\overrightarrow n = ( - 6).0 + 1.2 = 0 + 2 = 2\)
Ta có \(10\overrightarrow m = ( - 60;10)\) và \( - 4\overrightarrow n = (0; - 8)\) nên \(\left( {10\overrightarrow m } \right).\left( { - 4\overrightarrow n } \right) = ( - 60).0 + 10.( - 8) = 0 - 80 = - 80\)
Một thiết bị thăm dò đáy biển đang lặn với vận tốc \(\overrightarrow v = \left( {10; - 8} \right)\) (hình 8). Cho biết vận tốc của dòng hải lưu vùng biển là \(\overrightarrow w = \left( {3,5;0} \right)\). Tìm tọa dộ của vectơ tổng hai vận tốc \(\overrightarrow v \) và \(\overrightarrow w \)
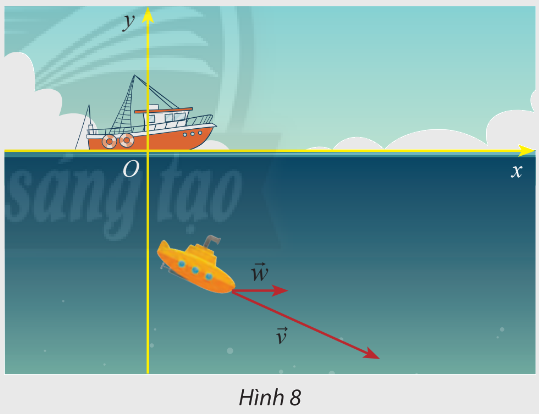
Phương pháp giải:
Với \(\overrightarrow v = \left( {{v_1};{v_2}} \right),\overrightarrow w = \left( {{w_1};{w_2}} \right)\) thì \(\overrightarrow v + \overrightarrow w \) là \(\left( {{v_1} + {w_1};{v_2} + {w_2}} \right)\)
Lời giải chi tiết:
\(\overrightarrow v + \overrightarrow w = (10 + 3,5;( - 8) + 0) = (13,5; - 8)\)
Vậy tọa độ của vectơ tổng hai vận tốc \(\overrightarrow v \) và \(\overrightarrow w \) là \((13,5; - 8)\)
Mục 2 của SGK Toán 10 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong hình học hoặc đại số. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, định lý và công thức liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2 trang 40, 41, đồng thời phân tích phương pháp giải và các lưu ý quan trọng.
Bài tập 1 thường là bài tập áp dụng trực tiếp kiến thức lý thuyết. Để giải bài tập này, học sinh cần:
(Lời giải chi tiết bài tập 1 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích và kết luận.)
Bài tập 2 có thể là bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng kiến thức một cách linh hoạt và sáng tạo. Để giải bài tập này, học sinh cần:
(Lời giải chi tiết bài tập 2 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích và kết luận.)
Bài tập 3 có thể là bài tập liên hệ thực tế, yêu cầu học sinh phải áp dụng kiến thức Toán học vào giải quyết các vấn đề trong cuộc sống. Để giải bài tập này, học sinh cần:
(Lời giải chi tiết bài tập 3 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích và kết luận.)
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi giải quyết các bài tập trong mục 2 trang 40, 41 SGK Toán 10 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Áp dụng lý thuyết cơ bản |
| Bài 2 | Vận dụng kiến thức linh hoạt |
| Bài 3 | Liên hệ thực tế |